
【题目】2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为( )
A.20B.25C.30D.40
科目:高中数学 来源: 题型:
【题目】光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度) |
|
|
|
|
|
户数 | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在该县居民中随机抽取10户,记其中年用电量不超过600度的户数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(Ⅱ)在总结试点经验的基础上,将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E![]() 的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
A.y=±![]() B.y=±
B.y=±![]() C.y=±2xD.y=±3x
C.y=±2xD.y=±3x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:
①若“![]() 或
或![]() ”为假命题,则
”为假命题,则![]() 均为假命题;
均为假命题;
②命题“若![]() 且
且![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() 且
且![]() ,则
,则![]() ”;
”;
③若![]() 是实数,则“
是实数,则“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
④命题“若![]() 则
则![]() ”的逆否命题为真命题.
”的逆否命题为真命题.
其中正确命题的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为准确把握市场规律,某公司对其所属商品售价进行市场调查和模型分析,发现该商品一年内每件的售价按月近似呈![]() 的模型波动(
的模型波动(![]() 为月份),已知3月份每件售价达到最高90元,直到7月份每件售价变为最低50元.则根据模型可知在10月份每件售价约为_____.(结果保留整数)
为月份),已知3月份每件售价达到最高90元,直到7月份每件售价变为最低50元.则根据模型可知在10月份每件售价约为_____.(结果保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
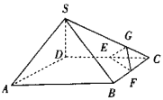
求证:(1)直线![]() 平面EFG;
平面EFG;
(2)直线![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com