
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,椭圆C上的一点P到
,椭圆C上的一点P到![]() ,
,![]() 的距离之和等于4.
的距离之和等于4.
(1)求椭圆C的标准方程;
(2)设![]() ,过椭圆C的右焦点
,过椭圆C的右焦点![]() 的直线与椭圆C交于A,B两点,若满足
的直线与椭圆C交于A,B两点,若满足![]() 恒成立,求m的最小值.
恒成立,求m的最小值.
【答案】(1)![]() (2)5
(2)5
【解析】
(1)利用椭圆的定义以及离心率求出![]() ,进而可写出椭圆的方程.
,进而可写出椭圆的方程.
(2)由(1)可知![]() ,设
,设![]() ,
,![]() ,利用向量数量积的坐标运算可得
,利用向量数量积的坐标运算可得![]() ,分类讨论设出直线方程,当直线l与x轴垂直或直线l不与x轴垂直时,将直线与椭圆联立,利用韦达定理可将
,分类讨论设出直线方程,当直线l与x轴垂直或直线l不与x轴垂直时,将直线与椭圆联立,利用韦达定理可将![]() 用
用![]() 的式子表示,然后再利用函数的单调性即可求解.
的式子表示,然后再利用函数的单调性即可求解.
解:(1)设椭圆的焦距为![]() ,
,
由题意可得,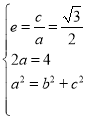 ,解得
,解得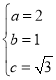 ,
,
∴椭圆C的标准方程为:![]() ;
;
(2)由(1)可知![]() ,
,
设![]() ,
,![]() ,则
,则
![]() ,
,![]() ,
,
![]() ,
,
①当直线l与x轴垂直时,直线l的方程为![]() ,得
,得![]() ,
,
代入得![]() ,
,![]() ,或
,或![]() ,
,![]() ,则
,则![]() ,
,
②当直线l不与x轴垂直时,设直线的方程为![]() ,
,
联立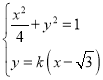 ,得
,得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
![]() ,
,
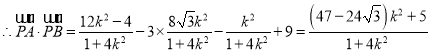
令![]() ,
,![]() ,则
,则![]() ,
,
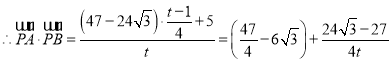 ,
,
又因函数![]() 在
在![]() 上是减函数,
上是减函数,
![]() ,
,
综上:m的最小值为5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
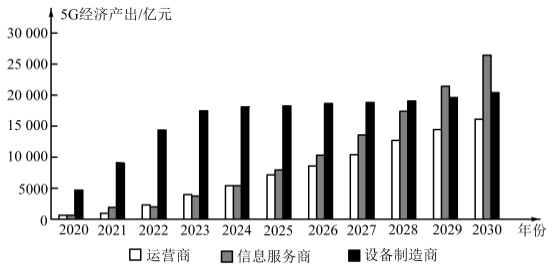
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求实数![]() 的值,使得
的值,使得![]() 为奇函数;
为奇函数;
(2)若关于![]() 的方程
的方程![]() 有两个不同实数解,求
有两个不同实数解,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对由![]() 和
和![]() 这两个数字组成的字符串,作如下规定:按从左向右的顺序,当第一个子串“
这两个数字组成的字符串,作如下规定:按从左向右的顺序,当第一个子串“![]() ”的最后一个
”的最后一个![]() 所在数位是第
所在数位是第![]() (
(![]() ,且
,且![]() )位,则称子串“
)位,则称子串“![]() ”在第
”在第![]() 位出现;再继续从第
位出现;再继续从第![]() 位按从左往右的顺序找子串“
位按从左往右的顺序找子串“![]() ”,若第二个子串“
”,若第二个子串“![]() ”的最后一个
”的最后一个![]() 所在数位是第
所在数位是第![]() 位(其中
位(其中![]() 且
且![]() ),则称子串“
),则称子串“![]() ”在第
”在第![]() 位出现;……;如此不断地重复下去.如:在字符串
位出现;……;如此不断地重复下去.如:在字符串![]() 中,子串“
中,子串“![]() ”在第
”在第![]() 位和第
位和第![]() 位出现,而不是在第
位出现,而不是在第![]() 位和第
位和第![]() 位出现.记在
位出现.记在![]() 位由
位由![]() 组成的所有字符串中,子串“
组成的所有字符串中,子串“![]() ”在第
”在第![]() 位出现的字符串的个数为
位出现的字符串的个数为![]() .
.
(1)求![]() 的值;
的值;
(2)求证:对任意的正整数![]() ,
,![]() 是
是![]() 的倍数.
的倍数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生态农场有一矩形地块,地块内有一半圆形池塘(如图所示),其中![]() 百米,
百米,![]() 百米,半圆形池塘的半径为1百米,圆心
百米,半圆形池塘的半径为1百米,圆心![]() 与线段
与线段![]() 的中点重合,半圆与
的中点重合,半圆与![]() 的左侧交点为
的左侧交点为![]() .该农场计划分别在
.该农场计划分别在![]() 和
和![]() 上各选一点
上各选一点![]() ,修建道路
,修建道路![]() ,要求
,要求![]() 与半圆相切.
与半圆相切.
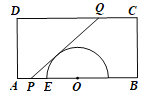
(1)若![]() ,求该道路的总长;
,求该道路的总长;
(2)若![]() 为观光道路,修建费用是4万元/百米,
为观光道路,修建费用是4万元/百米,![]() 为便道,修建费用是1万元/百米,求修建观光道路与便道的总费用的最小值.
为便道,修建费用是1万元/百米,求修建观光道路与便道的总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.
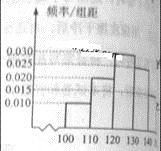
(Ⅰ)将T表示为x的函数
(Ⅱ)根据直方图估计利润T不少于57000元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x![]() ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110![]() ,求T的数学期望.
,求T的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
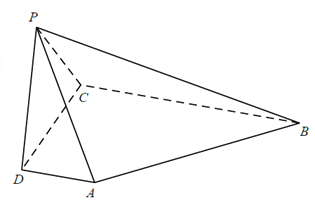
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,人们支付方式发生巨大转变,使用移动支付购买商品已成为一部分人的消费习惯,某企业为了解该企业员工![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月
两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 两种支付方式都使用过的概率为_______________
两种支付方式都使用过的概率为_______________
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com