
【题目】已知四面体![]() 的棱长满足
的棱长满足![]() ,
,![]() ,现将四面体
,现将四面体![]() 放入一个主视图为等边三角形的圆锥中,使得四面体
放入一个主视图为等边三角形的圆锥中,使得四面体![]() 可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
【答案】![]()
【解析】
若满足题意,则四面体的外接球应该内切于圆锥即可.先求得四面体外接球的半径,再根据该球内切于圆锥,即可求得圆锥侧面积的最小值.
若满足题意,则四面体的外接球应该内切于圆锥即可.
为逻辑清晰,我们将问题主要分为两步.
第一步:求得四面体![]() 外接球半径.
外接球半径.
记![]() 外心为
外心为![]() ,过
,过![]() 作平面
作平面![]() 的垂线
的垂线![]() ,
,
记外接球球心为![]() ,连接
,连接![]() .
.
则外接球半径![]() .下面求解
.下面求解![]() .
.

在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,
,
则由同角三角函数关系可得![]() .
.
故![]() 外接圆半径
外接圆半径![]() .
.
将![]() 的图形单独抽取出来,取
的图形单独抽取出来,取![]() 中点为
中点为![]() .如上面由图所示:
.如上面由图所示:
容易知: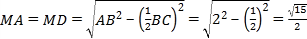 .
.
在![]() 中,因为
中,因为![]() ,
,![]() ,
,
故可得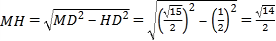 ,
,
![]() .
.
故可得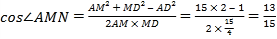 .
.
又因为![]() ,
,
解得![]() .
.
在![]() 中,容易得
中,容易得![]() .
.
故可得![]() .
.
在![]() 中,
中,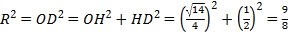 .
.
故可得四面体![]() 外接球半径
外接球半径![]() .
.
第二步:根据外接球半径和圆锥的关系,求得圆锥的母线和底面圆半径.
若满足题意,则该外接球应该内切于圆锥,
作出轴截面的平面图,其中![]() 点为
点为![]() 的中点,如下所示:
的中点,如下所示:

该截面图中![]() .
.
由题可知![]() 为等边三角形,故可得
为等边三角形,故可得![]() ;
;
在![]() 中,
中,![]() ,解得
,解得![]() .
.
故可得圆锥的底面圆半径为![]() .母线长
.母线长![]() .
.
故可得圆锥的侧面积为![]()
![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]()
(1)求![]() 的轨迹
的轨迹![]()
(2)过轨迹![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,设直线
,设直线![]() 的斜率分别是
的斜率分别是![]() ,试问在三个斜率都存在且不为0的条件下,
,试问在三个斜率都存在且不为0的条件下, 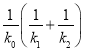 是否是定值,请说明理由,并加以证明.
是否是定值,请说明理由,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.
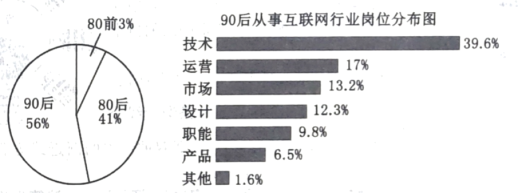
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有且仅有2个零点,对于下列4个结论:①在区间
上有且仅有2个零点,对于下列4个结论:①在区间![]() 上存在
上存在![]() ,满足
,满足![]() ;②
;②![]() 在区间
在区间![]() 有且仅有1个最大值点;③
有且仅有1个最大值点;③![]() 在区间
在区间![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() ,其中所有正确结论的编号是( )
,其中所有正确结论的编号是( )
A.①③B.①③④C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com