
【题目】已知三个点A(2,1)、B(3,2)、D(﹣1,4).
(1)求证: ![]() ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD两对角线所夹锐角的余弦值.
【答案】
(1)证明:A(2,1),B(3,2),D(﹣1,4).
∴ ![]() =(1,1),
=(1,1), ![]() =(﹣3,3).
=(﹣3,3).
又∵ ![]() =1×(﹣3)+1×3=0,
=1×(﹣3)+1×3=0,
∴ ![]() .
.
(2)解:∵ ![]() ,若四边形ABCD为矩形,则
,若四边形ABCD为矩形,则 ![]() .
.
设C点的坐标为(x,y),则有(1,1)=(x+1,y﹣4),
∴ ![]()
即 ![]()
∴点C的坐标为(0,5).
由于 ![]() =(﹣2,4),
=(﹣2,4), ![]() =(﹣4,2),
=(﹣4,2),
∴ ![]() =(﹣2)×(﹣4)+4×2=16,
=(﹣2)×(﹣4)+4×2=16, ![]() =2
=2 ![]() .
.
设对角线AC与BD的夹角为θ,则cosθ= ![]() =
= ![]() >0.
>0.
故矩形ABCD两条对角线所夹锐角的余弦值为 ![]() .
.
【解析】(1)运用平面向量的数量积得出 ![]() =1×(﹣3)+1×3=0,求解即可.(2)
=1×(﹣3)+1×3=0,求解即可.(2) ![]() .
. ![]() ,坐标得出点C的坐标为(0,5).再运用数量积求解得出cosθ=
,坐标得出点C的坐标为(0,5).再运用数量积求解得出cosθ= ![]() =
= ![]() >0.
>0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() ),其图象相邻两条对称轴之间的距离为
),其图象相邻两条对称轴之间的距离为 ![]() ,且函数f(x+
,且函数f(x+ ![]() )是偶函数,下列判断正确的是( )
)是偶函数,下列判断正确的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于点( ![]() ,0)d对称
,0)d对称
C.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
D.函数f(x)在[ ![]() ,π]上单调递增
,π]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角α﹣AB﹣β是直二面角,P为棱AB上一点,PQ、PR分别在平面α、β内,且∠QPB=∠RPB=45°,则∠QPR为( )
A.45°
B.60°
C.120°
D.150°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)若销售金额(单位:万元)不低于平均值![]() 的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC= ![]() ,SA=SC=SD=2.
,SA=SC=SD=2.
(I)求证:AC⊥SD;
(Ⅱ)求二面角A﹣SB﹣C的余弦值.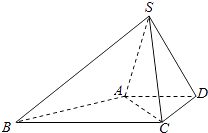
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式
(2)若bn=anlog ![]() an , Sn=b1+b2+b3+…+bn , 对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
an , Sn=b1+b2+b3+…+bn , 对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形ABC的顶点坐标A(﹣2,0),直角顶点B(0,﹣2 ![]() ),顶点C在x轴上,点P为线段OA的中点,三角形ABC外接圆的圆心为M.
),顶点C在x轴上,点P为线段OA的中点,三角形ABC外接圆的圆心为M. 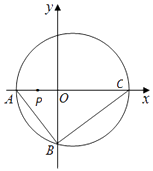
(1)求BC边所在直线方程;
(2)求圆M的方程;
(3)直线l过点P且倾斜角为 ![]() ,求该直线被圆M截得的弦长.
,求该直线被圆M截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com