在三棱锥
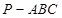
中,
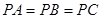
,底面
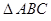
是正三角形,
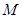
、
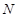
分别是侧棱
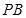
、
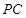
的中点.若平面
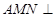
平面
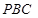
,则平面
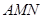
与平面
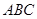
所成二面角(锐角)的余弦值等于( )

试题分析:设

的中点为
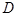
,
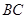
的中点为
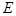
,连接
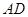
,
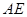
,
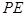
.在平面
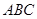
内作
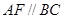
,则平面
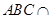
平面
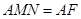
.
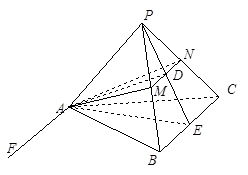
由已知得
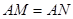
.
∴
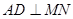
.
∵平面
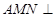
平面
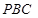
,
∴

平面
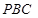
.
∴

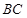
,

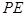
.
∵
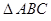
是等边三角形,
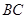
的中点为
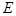
,
∴
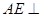
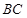
. ∵
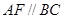
,
∴
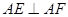
,
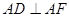
.
∴
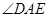
是平面
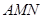
与平面
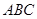
所成二面角(锐角)的平面角.
设等边
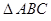
的边长为
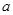
,侧棱长为
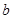
.
∵
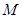
、
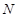
分别是侧棱
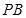
、
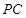
的中点,
∴
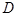
是
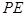
的中点.
∵

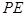
,∴
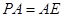
.
∴
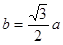
.
∴
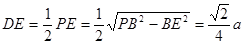
.
∴
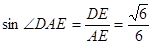
.
∴
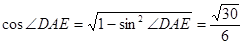
.故选A.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
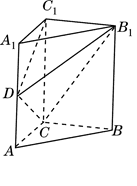
如图,三棱柱
的底面是边长为
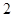
的正三角形,侧棱垂直于底面,侧棱长为
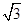
,D为棱
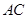
的中点。
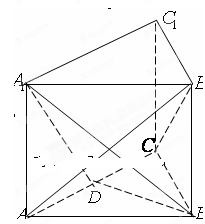
(Ⅰ)求证:
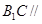
平面
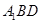
;
(Ⅱ)求二面角
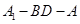
的大小.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,在四棱锥
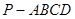
中,底面
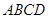
是矩形,
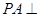
底面
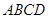
,
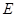
是
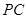
的中点,已知
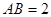
,
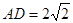
,
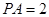
,
求:(Ⅰ)三角形
的面积;(II)三棱锥
的体积
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,在四棱锥

中,

⊥底面

,四边形

是直角梯形,

⊥

,

∥

,

.

(Ⅰ)求证:平面

⊥平面

;
(Ⅱ)若二面角

的余弦值为

,求

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,在直三棱柱(即侧棱与底面垂直的三棱柱)
中,
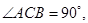
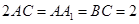
,
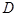
为
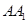
的中点

(I)求证:平面
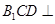
平面
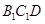
;
(II)求
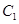
到平面
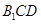
的距离.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
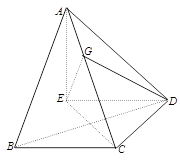
如图,在三棱锥
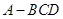
中,
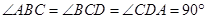
,
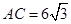
,
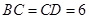
,设顶点A在底面
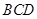
上的射影为R.
(Ⅰ)求证:
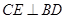
;
(Ⅱ)设点
在棱
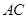
上,且
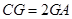
,试求二面角
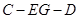
的余弦值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,三棱柱
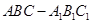
的所有棱长都为
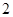
,且
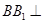
平面
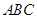
,
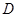
为
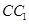
中点.
(Ⅰ)求证:
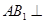
面
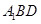
;
(Ⅱ)求二面角
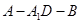
的大小的余弦值;
(Ⅲ)求点
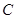
到平面
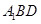
的距离.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
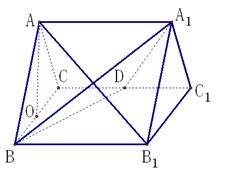
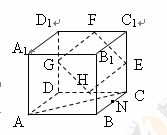
如图,在正四棱柱
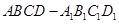
中,
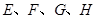
分别是
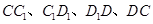
的中点,
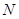
是
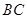
的中点,点
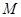
在四边形
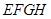
上或其内部运动,且使
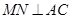
,对于下列命题:①点
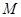
可以与点
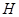
重合;②点
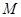
可以与点
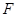
重合;③点
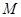
可以在线段
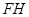
上;④点
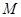
可以与点
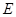
重合.
其中正确命题的序号是
(把你认为正确命题的序号都填上).
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在正四面体
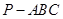
(所有棱长都相等)中,
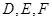
分别是
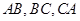
的中点,下面四个结论中不成立的是( )
查看答案和解析>>

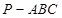 中,
中,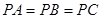 ,底面
,底面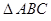 是正三角形,
是正三角形,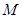 、
、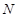 分别是侧棱
分别是侧棱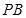 、
、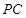 的中点.若平面
的中点.若平面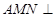 平面
平面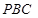 ,则平面
,则平面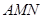 与平面
与平面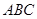 所成二面角(锐角)的余弦值等于( )
所成二面角(锐角)的余弦值等于( )




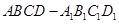 中,
中,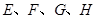 分别是
分别是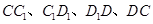 的中点,
的中点,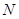 是
是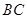 的中点,点
的中点,点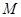 在四边形
在四边形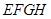 上或其内部运动,且使
上或其内部运动,且使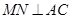 ,对于下列命题:①点
,对于下列命题:①点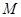 可以与点
可以与点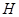 重合;②点
重合;②点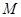 可以与点
可以与点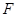 重合;③点
重合;③点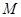 可以在线段
可以在线段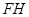 上;④点
上;④点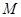 可以与点
可以与点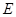 重合.
重合.