
【题目】 如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?

科目:高中数学 来源: 题型:
【题目】设a,b,c分别是![]() 的三条边,且
的三条边,且![]() .我们知道,如果
.我们知道,如果![]() 为直角三角形,那么
为直角三角形,那么![]() (勾股定理).反过来,如果
(勾股定理).反过来,如果![]() ,那么
,那么![]() 为直角三角形(勾股定理的逆定理).由此可知,
为直角三角形(勾股定理的逆定理).由此可知,![]() 为直角三角形的充要条件是
为直角三角形的充要条件是![]() .请利用边长a,b,c分别给出
.请利用边长a,b,c分别给出![]() 为锐角三角形和钝角三角形的一个充要条件,并证明.
为锐角三角形和钝角三角形的一个充要条件,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
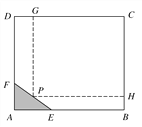
【题目】如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,问如何设计才能使公园占地面积最大,求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题已知![]() 或
或![]() ,
,![]() ,则
,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
②“函数![]() 的最小正周期为
的最小正周期为![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 在
在![]() 上恒成立
上恒成立![]() 在
在![]() 上恒成立;
上恒成立;
④“平面向量![]() 与
与![]() 的夹角是钝角”的充要条件是“
的夹角是钝角”的充要条件是“![]() ”
”
⑤命题![]() 函数
函数![]() 的值域为
的值域为![]() ,命题
,命题![]() 函数
函数![]() 是减函数.若
是减函数.若![]() 或
或![]() 为真命题,
为真命题,![]() 且
且![]() 为假命题,则实数
为假命题,则实数![]() 的取值范围是
的取值范围是![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2(x+![]() )-2
)-2![]() cos(x-
cos(x-![]() )-5a+2.
)-5a+2.
(1)设t=sinx+cosx,将函数f(x)表示为关于t的函数g(t),求g(t)的解析式;
(2)对任意x∈[0,![]() ],不等式f(x)≥6-2a恒成立,求a的取值范围.
],不等式f(x)≥6-2a恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
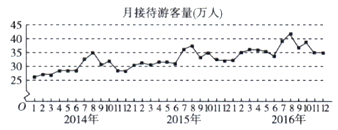
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com