
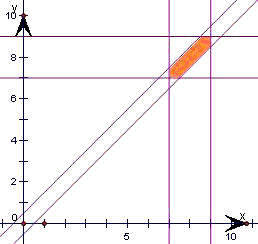
 解:由题意知本题是一个几何概型,设事件A为“两人能会面”,
解:由题意知本题是一个几何概型,设事件A为“两人能会面”, }
} =
= ,
, ÷4=
÷4= .
. },算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2009年浙江省台州市临海市灵江中学高二年级(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com