
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
注:年份代码1﹣7分别对应年份2008﹣2014.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: ![]() yi=9.32,
yi=9.32, ![]() tiyi=40.17,
tiyi=40.17, =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:  ,回归方程
,回归方程 ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
, ![]() .
.
【答案】
(1)
解:由折线图看出,y与t之间存在较强的正相关关系,理由如下:
∵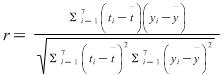 =
= 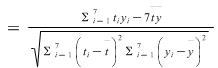 ≈
≈ ![]() ≈
≈![]() ≈0.996,
≈0.996,
∵0.996>0.75,
故y与t之间存在较强的正相关关系;
(2)
解: 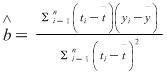 =
=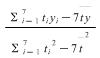 ≈
≈ ![]() ≈0.10,
≈0.10,![]() ≈1.331﹣0.10×4≈0.93,
≈1.331﹣0.10×4≈0.93,
∴y关于t的回归方程 ![]() =0.103+0.93,
=0.103+0.93,
2016年对应的t值为9,
故 ![]() =0.10×9+0.93=1.83,
=0.10×9+0.93=1.83,
预测2016年我国生活垃圾无害化处理量为1.83亿吨
【解析】(1)由折线图看出,y与t之间存在较强的正相关关系,将已知数据代入相关系数方程,可得答案;(2)根据已知中的数据,求出回归系数,可得回归方程,2016年对应的t值为9,代入可预测2016年我国生活垃圾无害化处理量.;本题考查的知识点是线性回归方程,回归分析,计算量比较大,计算时要细心.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象过点(2,4).
(1)求函数f(x)的解析式;
(2)设函数h(x)=4f(x)-kx-8在[5,8]上是单调函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )
A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2+bx+c(a≠0),满足条件f(x+1)-f(x)=2x(x∈R),且f(0)=1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x≥0时,f(x)≥mx-3恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com