
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
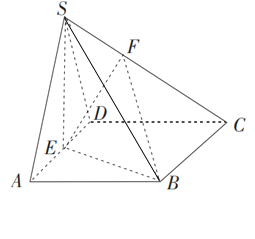
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() 右焦点为
右焦点为![]() ,直线
,直线![]() 是椭圆
是椭圆![]() 在点
在点![]() 处的切线.设点
处的切线.设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,且当
,且当![]() 时,
时, ![]() 是等腰三角形.
是等腰三角形.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设椭圆![]() 的长轴长等于
的长轴长等于![]() ,当点
,当点![]() 运动时,试判断以
运动时,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]()
![]() 的部分图象,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为
的部分图象,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为![]() ,点
,点![]() 是线段DM的中点.
是线段DM的中点.

(1)求函数![]() 的解析式及
的解析式及![]() 上的单调增区间;
上的单调增区间;
(2)若![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观察得到:在交通繁忙的时段内,某公路汽车的车流量![]() (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度![]() (千米/小时)之间的函数关系为
(千米/小时)之间的函数关系为![]()
(1)在该时段内,当汽车的平均速度![]() 为多少时,车流量最大,最大车流量为多少?(精确到0.1千辆/小时)
为多少时,车流量最大,最大车流量为多少?(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试后,对全班同学的数学成绩进行整理,得到表:
分数段 |
|
|
|
|
人数 | 5 | 15 | 20 | 10 |
将以上数据绘制成频率分布直方图后,可估计出本次考试成绩的中位数是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ABC的三个角A,B,C所对的边分别是a,b,c,向量
ABC的三个角A,B,C所对的边分别是a,b,c,向量![]() =(2,-1),
=(2,-1),![]() =(sinBsinC,
=(sinBsinC,![]() +2cosBcosC),且
+2cosBcosC),且![]() ⊥
⊥![]() .
.
(1)求角A的大小;
(2)现给出以下三个条件:①B=45;②2sinC-(![]() +1)sinB=0;③a=2.试从中再选择两个条件以确定
+1)sinB=0;③a=2.试从中再选择两个条件以确定![]() ABC,并求出所确定的
ABC,并求出所确定的![]() ABC的面积.
ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若数列![]() 满足
满足![]() ,
, ![]() ,记
,记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】试题分析:(Ⅰ)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)当
的减区间;(Ⅱ)当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,先证明因此
显然不成立,先证明因此![]() 时,
时, ![]() 在
在![]() 上恒成立,再证明当
上恒成立,再证明当![]() 时不满足题意,从而可得结果;(III)先求出等差数列的前
时不满足题意,从而可得结果;(III)先求出等差数列的前![]() 项和为
项和为![]() ,结合(II)可得
,结合(II)可得![]() ,各式相加即可得结论.
,各式相加即可得结论.
试题解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函数
(舍去),所以函数![]() 的单调递减区间为
的单调递减区间为 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,因此
显然不成立,因此![]() .
.
令![]() ,则
,则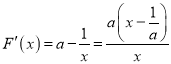 ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 时,
时, ![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
∴![]() ,不满足题意.
,不满足题意.
综上,不等式![]() 在
在![]() 上恒成立时,实数
上恒成立时,实数![]() 的取值范围是
的取值范围是![]() .
.
(III)证明:由![]() 知数列
知数列![]() 是
是![]() 的等差数列,所以
的等差数列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 将以上各式左右两边分别相加,得
. 将以上各式左右两边分别相加,得
![]() .因为
.因为![]()
所以![]()
所以![]() .
.
【题型】解答题
【结束】
22
【题目】已知直线![]() , (
, (![]() 为参数,
为参数, ![]() 为倾斜角).以坐标原点为极点,
为倾斜角).以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅰ)将曲线![]() 的直角坐标方程化为极坐标方程;
的直角坐标方程化为极坐标方程;
(Ⅱ)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com