Question

设f(x)＝a ln x＋＋x＋1，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线垂直于y轴．(1)求a的值；(2)求函数f(x)的极值．

 

Answer 1

【答案】

（1）a＝－1.

（2）f(x)在x＝1处取得极小值f(1)＝3，无极大值．

【解析】

试题分析：解：(1)因f(x)＝a ln x＋＋x＋1，

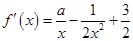故.            (2分)

由于曲线y＝f(x)在点(1，f(1))处的切线垂直于y轴，故该切线斜率为0，即f′(1)＝0，从而a－＋＝0，解得a＝－1.   （4分）

(2)由(1)知f(x)＝-ln x＋＋x＋1 (x＞0)，

令f′(x)＝0，解得x₁＝1，x₂＝－ (因x₂＝－不在定义域内，舍去)．（6分）

当x∈(0,1)时，f′(x)＜0，故f(x)在(0,1)上为减函数；

当x∈(1，＋∞)时，f′(x)＞0，故f(x)在(1，＋∞)上为增函数．

故f(x)在x＝1处取得极小值f(1)＝3，无极大值．             (10分)

考点：导数的几何意义的运用，以及极值

点评：运用导数的符号判定函数的单调性，求解极值，属于基础题。