
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1 , a14=b4 .
(1)求{an}的通项公式;
(2)设cn=an+bn , 求数列{cn}的前n项和.
【答案】
(1)解:设{an}是公差为d的等差数列,
{bn}是公比为q的等比数列,
由b2=3,b3=9,可得q= ![]() =3,
=3,
bn=b2qn﹣2=33n﹣2=3n﹣1;
即有a1=b1=1,a14=b4=27,
则d= ![]() =2,
=2,
则an=a1+(n﹣1)d=1+2(n﹣1)=2n﹣1
(2)解:cn=an+bn=2n﹣1+3n﹣1,
则数列{cn}的前n项和为
(1+3+…+(2n﹣1))+(1+3+9+…+3n﹣1)= ![]() n2n+
n2n+ ![]()
=n2+ ![]() .
.
【解析】1、由等比数列和等差数列的定义可求得公比q=3,公差d=2,即得等差数列的通项公式。
2、根据题意把数列{cn}的前n项和分解成为一个等差数列前2n-1项的和和一个等比数列前2n-1项的和,利用公式求得。


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,直l线l的参数方程为 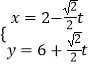 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=10cosθ.
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=10cosθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A、B,若点P的坐标为(2,6),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=4sinωxsin(ωx+ ![]() )﹣1(ω>0),f(x)的最小正周期为π.
)﹣1(ω>0),f(x)的最小正周期为π.
(Ⅰ)当x∈[0, ![]() ]时,求f(x)的最大值;
]时,求f(x)的最大值;
(Ⅱ)请用“五点作图法”画出f(x)在[0,π]上的图象.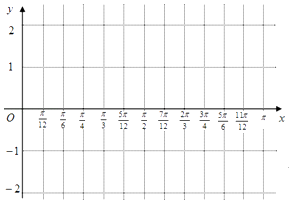
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,我们的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题.某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产该型号空气净化器x(百台),其总成本为P(x)(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本).销售收入Q(x)(万元)满足Q(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
(1)求利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且n+1=1+Sn对一切正整数n恒成立.
(1)试求当a1为何值时,数列{an}是等比数列,并求出它的通项公式;
(2)在(1)的条件下,当n为何值时,数列 ![]() 的前n项和Tn取得最大值.
的前n项和Tn取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校一模考试数学测试成绩的茎叶图和频率分布直方图都受到不同程序的破坏,可见部分如下
试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在 ![]() 之间的频数;
之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于 ![]() ,
, ![]() ,和
,和 ![]() 分数段的试卷中抽取8份进行分析,再从中任选2人进行交流,求交流的2名学生中,恰有一名成绩位于
分数段的试卷中抽取8份进行分析,再从中任选2人进行交流,求交流的2名学生中,恰有一名成绩位于 ![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1与x轴交于A、B两点,过椭圆上一点P(x0 , y0)(P不与A、B重合)的切线l的方程为
=1与x轴交于A、B两点,过椭圆上一点P(x0 , y0)(P不与A、B重合)的切线l的方程为 ![]() +
+ ![]() =1,过点A、B且垂直于x轴的垂线分别与l交于C、D两点,设CB、AD交于点Q,则点Q的轨迹方程为 .
=1,过点A、B且垂直于x轴的垂线分别与l交于C、D两点,设CB、AD交于点Q,则点Q的轨迹方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com