
【题目】若数据x1 , x2 , x3 , x4 , x5的方差为3,则数据2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差为 .
【答案】12
【解析】解:依题意,得 ![]() =
= ![]() (x1+x2+x3+x4+x5),
(x1+x2+x3+x4+x5),
∴2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数为![]() =
= ![]() [(2x1+1)+(2x2+1)+(2x3+1)+(2x4+1)+(2x5+1)]
[(2x1+1)+(2x2+1)+(2x3+1)+(2x4+1)+(2x5+1)]
=2× ![]() (x1+x2+x3+x4+x5)+1=2
(x1+x2+x3+x4+x5)+1=2 ![]() +1,
+1,
∵数据x1 , x2 , x3 , x4 , x5的方差为
S2= ![]() [(x1﹣
[(x1﹣ ![]() )2+(x2﹣
)2+(x2﹣ ![]() )2+(x3﹣
)2+(x3﹣ ![]() )2+(x4﹣
)2+(x4﹣ ![]() )2+(x5﹣
)2+(x5﹣ ![]() )2]=3,
)2]=3,
∴数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的方差为
S′2= ![]() [(2x1+1﹣2
[(2x1+1﹣2 ![]() ﹣1)2+(2x2+1﹣2
﹣1)2+(2x2+1﹣2 ![]() ﹣1)2+(2x3+1﹣2
﹣1)2+(2x3+1﹣2 ![]() ﹣1)2+(2x4+1﹣2
﹣1)2+(2x4+1﹣2 ![]() ﹣1)2+(2x5+1﹣2
﹣1)2+(2x5+1﹣2 ![]() ﹣1)2]
﹣1)2]
= ![]() [(x1﹣
[(x1﹣ ![]() )2+(x2﹣
)2+(x2﹣ ![]() )2+(x3﹣
)2+(x3﹣ ![]() )2+(x4﹣
)2+(x4﹣ ![]() )2+(x5﹣
)2+(x5﹣ ![]() )2]×4=3×4=12.
)2]×4=3×4=12.
所以答案是:12.
【考点精析】本题主要考查了极差、方差与标准差的相关知识点,需要掌握标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(1)+f(2)+f(3)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( ) 
A.f(x)= ![]() sin
sin ![]() x+1,S=2016
x+1,S=2016
B.f(x)= ![]() cos
cos ![]() x+1,S=2016
x+1,S=2016
C.f(x)= ![]() sin
sin ![]() x+1,S=2016.5
x+1,S=2016.5
D.f(x)= ![]() cos
cos ![]() x+1,S=2016.5
x+1,S=2016.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 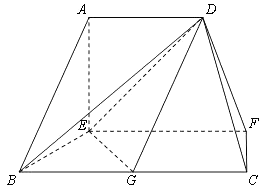
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为正的常数,函数f(x)=|ax﹣x2|+lnx.
(1)若a=2,求函数f(x)的单调递增区间;
(2)设g(x)= ![]() ,求g(x)在区间[1,e]上的最小值.(e≈2.71828为自然对数的底数)
,求g(x)在区间[1,e]上的最小值.(e≈2.71828为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c的图像如图,直线y=0在原点处与函数图像相切,且此切线与函数图像所围成的区域(阴影)面积为 ![]() .
. 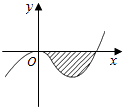
(1)求f(x)的解析式
(2)若常数m>0,求函数f(x)在区间[﹣m,m]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最未打的数学家之一,他所著的《四元玉鉴》卷中“如像招数一五间”,有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日?”.其大意为:“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始,每天派出的人数比前一天多7人,修筑堤坝的每人每天发大米3升,共发出大米40392升,问修筑堤坝多少天”.在这个问题中,前5天应发大米( )
A. 894升 B. 1170升 C. 1275升 D. 1457升
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com