
【题目】设双曲线x2﹣ ![]() =1的左、右焦点分别为F1、F2 , 若点P在双曲线上,且△F1PF2为锐角三角形,则|PF1|+|PF2|的取值范围是 .
=1的左、右焦点分别为F1、F2 , 若点P在双曲线上,且△F1PF2为锐角三角形,则|PF1|+|PF2|的取值范围是 .
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】设数列A: ![]() ,
, ![]() ,…
,… ![]() (N≥2)。如果对小于n(2≤n≤N)的每个正整数k都有
(N≥2)。如果对小于n(2≤n≤N)的每个正整数k都有 ![]() <
< ![]() ,则称n是数列A的一个“G时刻”。记“G(A)是数列A 的所有“G时刻”组成的集合。
,则称n是数列A的一个“G时刻”。记“G(A)是数列A 的所有“G时刻”组成的集合。
(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;
(2)证明:若数列A中存在 ![]() 使得
使得 ![]() >
> ![]() ,则G(A)
,则G(A) ![]()
![]() ;
;
(3)证明:若数列A满足 ![]() -
- ![]() ≤1(n=2,3, …,N),则GA.的元素个数不小于
≤1(n=2,3, …,N),则GA.的元素个数不小于 ![]() -
- ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)求该博物馆支付总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,A1A=AB=6,D为AC中点.
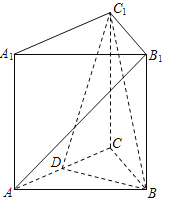
(1)求三棱锥C1﹣BCD的体积;
(2)求证:平面BC1D⊥平面ACC1A1;
(3)求证:直线AB1∥平面BC1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求证:“如果直线![]() 过点
过点![]() ,那么
,那么![]() ”是真命题;
”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
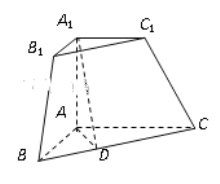
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)证明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
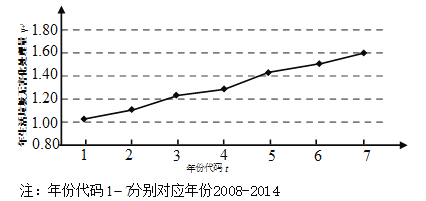
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请建立
的关系,请建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(2)预测2018年我国生活垃圾无害化处理量.
附注:
参考公式:设具有线性相关关系的两个变量![]() 的一组观察值为
的一组观察值为![]() ,
,
则回归直线方程![]() 的系数为:
的系数为:
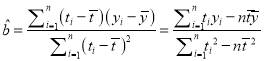 ,
, ![]() .
.
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题有__________.
①回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
②将一组数据的每个数据都加一个相同的常数后,方差不变;
③用相关指数![]() 来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
④若分类变量![]() 和
和![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 越大,则“
越大,则“![]() 与
与![]() 相关”的可信程度越小;
相关”的可信程度越小;
⑤.对于自变量![]() 和因变量
和因变量![]() ,当
,当![]() 取值一定时,
取值一定时, ![]() 的取值具有一定的随机性,
的取值具有一定的随机性, ![]() ,
, ![]() 间的这种非确定关系叫做函数关系;
间的这种非确定关系叫做函数关系;
⑥.残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适;
⑦.两个模型中残差平方和越小的模型拟合的效果越好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com