
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 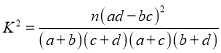 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)计算k2,与2.027比较大小得出结论,
(2)根据分层抽样即可求出经常使用共享单车和偶尔或不用共享单车的人数,)设这5人中,经常使用共享单车的3人分别为a,b,c;偶尔或不用共享单车的2人分别为d,e,根据古典概率公式计算即可.
试题解析:
(1)由列联表可知: ![]() ,
,
因为![]() ,
,
所以能在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关.
市使用共享单车情况与年龄有关.
(2)依题意可知,所抽取的5名30岁以上的网友中,经常使用共享单车的有![]() (人),偶尔或不用共享单车的有
(人),偶尔或不用共享单车的有![]() (人).
(人).
设这5人中,经常使用共享单车的3人分别为![]() ,
, ![]() ,
, ![]() ;偶尔或不用共享单车的2人分别为
;偶尔或不用共享单车的2人分别为![]() ,
, ![]() .
.
则从5人中选出2人的所有可能结果为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共10种,
共10种,
其中没有1人经常使用共享单车的可能结果为![]() 共1种,
共1种,
故选出的2人中至少有1人经常使用共享单车的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:
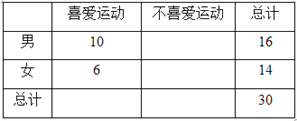
(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.
(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: 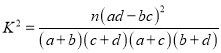
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前![]() 项和为
项和为![]() ,数列{bn},{cn}满足
,数列{bn},{cn}满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切![]() ,有bn≤λ≤cn,求证:数列{an}是等差数列.
,有bn≤λ≤cn,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品![]() 千件
千件![]() 并全部销售完,每千件的销售收入为
并全部销售完,每千件的销售收入为![]() 万元,且
万元,且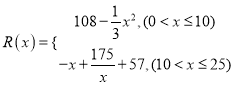 .
.
⑴ 写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
⑵ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入![]() 年总成本).
年总成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(I)证明:![]() 平面
平面![]() ;
;
(II)取![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,若存在,请求出
,若存在,请求出![]() 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到点
到点![]() 的距离最大值为4,过点
的距离最大值为4,过点![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
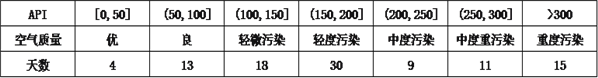
记某企业每天由空气污染造成的经济损失T(单位:元),空气质量指数API为![]() .在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为200元,当API为200时,造成的经济损失为400元);当API大于300时造成的经济损失为2000元.
.在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为200元,当API为200时,造成的经济损失为400元);当API大于300时造成的经济损失为2000元.
(1)试写出函数T(![]() )的表达式:
)的表达式:
(2)试估计在本年内随机抽取一天,该天经济损失大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
附: 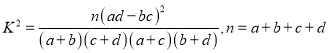
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com