
给出下列命题,其中正确命题的序号是 (填序号)。
(1)已知椭圆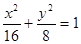 两焦点为
两焦点为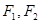 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点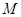 ,使得
,使得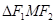 为直角三角形;
为直角三角形;
(2)已知直线 过抛物线
过抛物线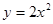 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于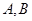 两点,则
两点,则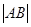 的最小值为2;
的最小值为2;
(3)若过双曲线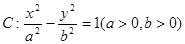 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为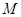 ,
,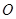 为坐标原点,则
为坐标原点,则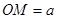 ;
;
(4)已知⊙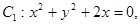 ⊙
⊙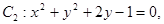 则这两圆恰有2条公切线。
则这两圆恰有2条公切线。
( 1) ( 3)( 4)
解析试题分析:椭圆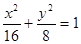 的两个焦点为F1(-2
的两个焦点为F1(-2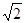 ,0),F2(2
,0),F2(2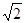 ,0),当F1M垂直于x 轴时,这样的点M有2个.当MF2垂直于x 轴时,这样的点M有2个.当∠F1MF2 为直角时,点M恰是椭圆短轴的端点(0,,2
,0),当F1M垂直于x 轴时,这样的点M有2个.当MF2垂直于x 轴时,这样的点M有2个.当∠F1MF2 为直角时,点M恰是椭圆短轴的端点(0,,2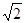 ),这样的点M有2个,综上,这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形,故①正确.
),这样的点M有2个,综上,这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形,故①正确.
因为过抛物线y=2x2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为抛物线的通径2p,由抛物线y=2x2的方程即x2=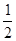 y 知,p=
y 知,p=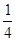 ,2p=
,2p=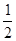 ,则|AB|的最小值为
,则|AB|的最小值为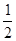 ,故②不正确.
,故②不正确.
因为双曲线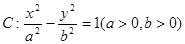 的一个焦点为(c,0),一条渐近线的方程 y=
的一个焦点为(c,0),一条渐近线的方程 y=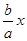 ,故垂线方程为 y-0=-
,故垂线方程为 y-0=-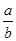 (x-c),它与渐近线 y=
(x-c),它与渐近线 y=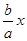 的交点M(
的交点M(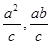 ),所以MO=a,故③正确.
),所以MO=a,故③正确.
因为⊙C1:x2+y2+2x=0,即 (x+1)2+y2=1,表示圆心为(-1,0),半径等于1的圆;⊙C2:x2+y2+2y-1="0" 即,x2+(y+1)2=2,表示圆心为(0,-1),半径等于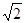 的圆.两圆的圆心距等于
的圆.两圆的圆心距等于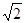 ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线有2条,故④正确.
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线有2条,故④正确.
故答案为:①③④.
考点:椭圆的简单性质;抛物线的简单性质;双曲线的简单性质;圆与圆的位置关系。
点评:掌握圆锥曲线的性质是解题的前提,灵活应用圆锥曲线的性质是解题的关键。属于中档题。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com