
【题目】已知函数f(x)=1﹣ ![]() (x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
(x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
A.![]()
B.![]()
C.![]() 且m≠0
且m≠0
D.![]()
【答案】B
【解析】解:∵函数f(x)=1﹣ ![]() (x>0)为定义域内的增函数,
(x>0)为定义域内的增函数,
要使y=f(x)的定义域为(a,b)时,值域为(ma,mb),
则 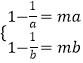 ,
,
即a,b为方程 ![]() 的两个实数根.
的两个实数根.
整理得mx2﹣x+1=0有两个不等的实数根.
∴m≠0.
则△=(﹣1)2﹣4m>0,解得m< ![]() .
.
又由原题给出的区间可知m>0.
∴实数m的取值范围是 ![]() .
.
故选B.
【考点精析】关于本题考查的函数的定义域及其求法和函数的值域,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=(log2x)2﹣2alog2x+b(x>0).当x= ![]() 时,f(x)有最小值﹣1.
时,f(x)有最小值﹣1.
(1)求a与b的值;
(2)求满足f(x)<0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张邱建算经》是中国古代数学史上的杰作,该书中有首古民谣记载了一数列问题:“南山一棵竹, 竹尾风割断, 剩下三十节,一节一个圈. 头节高五寸①,头圈一尺三②.逐节多三分③,逐圈少分三④. 一蚁往上爬,遇圈则绕圈. 爬到竹子顶,行程是多远?”(注释:①第一节的高度为![]() 尺;②第一圈的周长为
尺;②第一圈的周长为![]() 尺;③每节比其下面的一节多
尺;③每节比其下面的一节多![]() 尺;④每圈周长比其下面的一圈少
尺;④每圈周长比其下面的一圈少![]() 尺) 问:此民谣提出的问题的答案是
尺) 问:此民谣提出的问题的答案是
A. ![]() 尺 B.
尺 B. ![]() 尺
尺
C. ![]() 尺 D.
尺 D. ![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣4x+3,若f(x)≥mx对任意的实数x≥2都成立,则实数m的取值范围是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x2﹣2ax)(a>0且a≠1)满足对任意的x1 , x2∈[3,4],且x1≠x2时,都有 ![]() >0成立,则实数a的取值范围是
>0成立,则实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是 , 若D1E⊥EC,则直线A1D与平面D1DE所成的角为 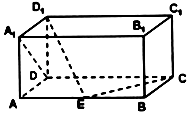
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , n∈N* , 已知a1=1,a2= ![]() ,a3=
,a3= ![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
(1)求a4的值.
(2)证明:{an﹣1﹣ ![]() an}为等比数列;
an}为等比数列;
(3)求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com