
【题目】已知定点![]() ,动点P是圆M:
,动点P是圆M:![]() 上的任意一点,线段NP的垂直平分线和半径MP相交于点Q.
上的任意一点,线段NP的垂直平分线和半径MP相交于点Q.
![]() 求
求![]() 的值,并求动点Q的轨迹C的方程;
的值,并求动点Q的轨迹C的方程;
![]() 若圆
若圆![]() 的切线l与曲线C相交于A,B两点,求
的切线l与曲线C相交于A,B两点,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为边长为2的菱形,∠DAB=60°,∠ADP=90°,面ADP⊥面ABCD,点F为棱PD的中点.
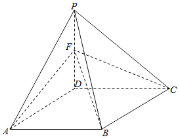
(1)在棱AB上是否存在一点E,使得AF∥面PCE,并说明理由;
(2)当二面角D﹣FC﹣B的余弦值为![]() 时,求直线PB与平面ABCD所成的角.
时,求直线PB与平面ABCD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的焦点弦的弦长为
轴的焦点弦的弦长为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,
,![]() 互相垂直,直线
互相垂直,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于点
交于点![]() ,
,![]() 两点,直线
两点,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.求
两点.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,右顶点为B,且满足
,右顶点为B,且满足![]()
![]() Ⅰ
Ⅰ![]() 求椭圆的离心率e;
求椭圆的离心率e;
![]() Ⅱ
Ⅱ![]() 设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点
设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点![]() ,问是否存在过
,问是否存在过![]() 的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
, ![]() ,点
,点![]() 满足:
满足: ![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
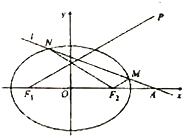
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若斜率为![]() (
(![]() )的直线
)的直线![]() 与
与![]() 轴、椭圆
轴、椭圆![]() 顺次相交于点
顺次相交于点![]() 、
、![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
①用表中字母列举出所有可能的结果;
②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
(2)节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com