
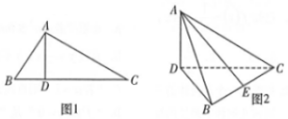
 如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.分析 (1)推导出AD⊥CD,AD⊥BD,从而AD⊥平面BCD,由此能证明平面ABD⊥平面BCD.
(2)取CD的中点F,连结EF,由EF∥BD,∠AEF是异面直线AE与BD所成角,由此能求出异面直线AE与BD所成的角.
解答 证明:(1)∵折起前AD是BC边上的高,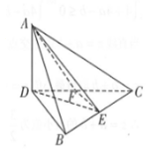
∴当折起后,AD⊥CD,AD⊥BD,
又CD∩BD=D,∴AD⊥平面BCD,
∵AD?平面ABD,
∴平面ABD⊥平面BCD.
解:(2)取CD的中点F,连结EF,由EF∥BD,
∴∠AEF是异面直线AE与BD所成角,
连结AF、DE,设BD=2,则EF=1,AD=2$\sqrt{3}$,CD=6,DF=3,
在Rt△ADF中,AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{21}$,
在△BCD中,由题设知∠BDC=60°,
则BC2=BD2+CD2-2BD•CD•cos60°=28,∴BC=2$\sqrt{7}$,
∴BE=$\sqrt{7}$,∴cos$∠CBD=\frac{1}{2\sqrt{7}}$,
在△BDE中,DE2=BD2+BE2-2BD•BE•cos∠CBD=13,
在Rt△ADE中,cos∠AEF=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\frac{A{E}^{2}+E{F}^{2}-A{F}^{2}}{2AE•EF}$=$\frac{1}{2}$,
∴∠AEF=60°,'
∴异面直线AE与BD所成的角为60°.
点评 本题考查面面垂直的证明,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,使得x2-1<0”的否定是:“?x∈R,均有x2-1>0” | |
| B. | “若x=3,则x2-2x-3=0”的否命题是:“若x≠3,则x2-2x-3≠0” | |
| C. | “存在四边相等的四边形不是正方形”是假命题 | |
| D. | “若cosx=cosy,则x=y”的逆否命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
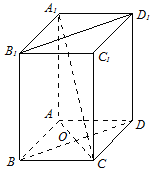 已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.
已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,2${\;}^{{x}_{0}}$>0 | B. | ?x0∈R,2${\;}^{{x}_{0}}$≤0 | C. | ?x∈R,2x<0 | D. | ?x∈R,2x≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+y2=2016 | B. | x2+(y-2)2=2016 | C. | (x+1)2+(y+1)2=2016 | D. | (x-1)2+(y-1)2=2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com