
 次预赛成绩记录如下:
次预赛成绩记录如下: 


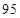
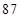 乙
乙 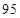
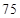


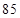
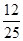 ;(3)①
;(3)①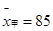 ,
, ;
;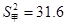 ,
,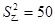 ;②甲的成绩较稳定,派甲参赛比较合适。
;②甲的成绩较稳定,派甲参赛比较合适。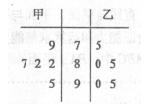 2分
2分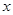 ,乙被抽到成绩为
,乙被抽到成绩为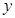 ,用数对
,用数对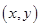 表示基本事件:
表示基本事件: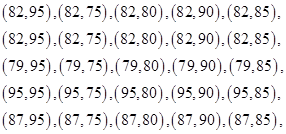
 4分
4分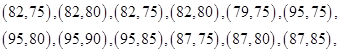 5分
5分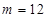 ,所以
,所以
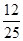 6分
6分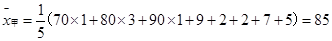 ,
,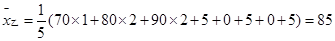
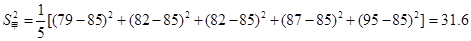
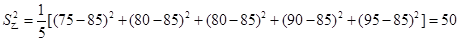 10分
10分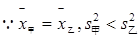 ,
,  甲的成绩较稳定,派甲参赛比较合适。 12分
甲的成绩较稳定,派甲参赛比较合适。 12分

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源:不详 题型:解答题
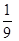 ,求甲在初赛中答题个数
,求甲在初赛中答题个数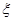 的分布列及数学期望
的分布列及数学期望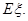 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 的把握认为对莫言作品的非常了解与性别有关?
的把握认为对莫言作品的非常了解与性别有关?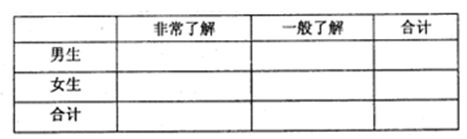

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
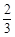 ,求甲在初赛中答题个数的分布列和数学期望.
,求甲在初赛中答题个数的分布列和数学期望.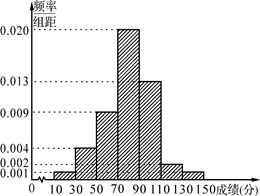
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
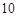 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;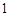 ;
;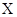 与
与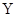 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“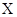 与
与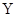 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )| A.①④ | B.②④ | C.①③ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 1.4 | 2.3 | 3.1 | 3.7 | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com