
【题目】为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着![]() 三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择
三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择![]() 三个项目的意向如下:
三个项目的意向如下:
扶贫项目 |
|
|
|
贫困户 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每个贫困户只能从自己已登记的选择意向中随机选取一项,且每个项目至多有两个贫困户选择,则甲乙两户选择同一个扶贫项目的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】已知有穷数列A:![]() (
(![]() 且
且![]() ).定义数列A的“伴生数列”B:
).定义数列A的“伴生数列”B:![]() ,其中
,其中 (
(![]() ),规定
),规定![]() ,
,![]() .
.
(1)写出下列数列的“伴生数列”:
①1,2,3,4,5;
②1,![]() ,1,
,1,![]() ,1.
,1.
(2)已知数列B的“伴生数列”C:![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]() ,且满足
,且满足![]() (
(![]() ,2,…,n).
,2,…,n).
(i)若数列B中存在相邻两项为1,求证:数列B中的每一项均为1;
(ⅱ)求数列C所有项的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用2与0两个数字排成7位的数码,其中“20”和“02”各至少出现两次(如0020020、2020200、0220220等),则这样的数码的个数是( )
A.54B.44C.32D.22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() (
(![]() )的各项均为正整数,且
)的各项均为正整数,且![]() .若对任意
.若对任意![]() ,存在正整数
,存在正整数![]() 使得
使得![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .
.
(1)判断数列![]() 与数列
与数列![]() 是否具有性质
是否具有性质![]() ;(只需写出结论)
;(只需写出结论)
(2)若数列![]() 具有性质
具有性质![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)若集合![]() ,且
,且![]() (任意
(任意![]() ,
,![]() ).求证:存在
).求证:存在![]() ,使得从
,使得从![]() 中可以选取若干元素(可重复选取)组成一个具有性质
中可以选取若干元素(可重复选取)组成一个具有性质![]() 的数列.
的数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
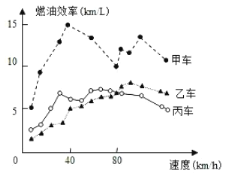
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用乙车比用丙车更省油
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com