
【题目】已知曲线C1: ![]() (参数θ∈R),以坐标原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
(参数θ∈R),以坐标原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为 ![]() ,点Q的极坐标为
,点Q的极坐标为 ![]() .
.
(1)将曲线C2的极坐标方程化为直角坐标方程,并求出点Q的直角坐标;
(2)设P为曲线C1上的点,求PQ中点M到曲线C2上的点的距离的最小值.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 与
与![]() 均是以
均是以![]() 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上的任意一点.
上的任意一点.

(1)求证:![]() :
:
(2)在平面![]() 中,是否总存在与平面
中,是否总存在与平面![]() 平行的直线?若存在,请作出图形并说明:若不存在,请说明理由.
平行的直线?若存在,请作出图形并说明:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D. 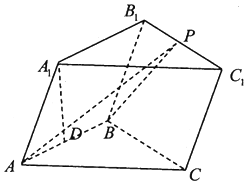
(1)证明:平面AA1B1B⊥平面BB1C1C;
(2)设P为B1C1上一点,且 ![]() ,求二面角A1﹣AB﹣P的正弦值.
,求二面角A1﹣AB﹣P的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.已知点
轴的正半轴为极轴建立极坐标系.已知点![]() 的直角坐标为
的直角坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,求直线
,求直线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抽样统计甲、乙两名学生的5次训练成绩(单位:分),结果如下:
学生 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲 | 65 | 80 | 70 | 85 | 75 |
乙 | 80 | 70 | 75 | 80 | 70 |
则成绩较为稳定(方差较小)的那位学生成绩的方差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求销量![]() (件)关于单价
(件)关于单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(2)若单价定为10元,估计销量为多少件;
(3)根据销量![]() 关于单价
关于单价![]() 的线性回归方程,要使利润
的线性回归方程,要使利润![]() 最大,应将价格定为多少?
最大,应将价格定为多少?
参考公式: ,
,![]() .参考数据:
.参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d不为0,且 ![]() ,
, ![]() ,…,
,…, ![]() ,…(k1<k2<…<kn<…)成等比数列,公比为q.
,…(k1<k2<…<kn<…)成等比数列,公比为q.
(1)若k1=1,k2=3,k3=8,求 ![]() 的值;
的值;
(2)当 ![]() 为何值时,数列{kn}为等比数列;
为何值时,数列{kn}为等比数列;
(3)若数列{kn}为等比数列,且对于任意n∈N* , 不等式 ![]() 恒成立,求a1的取值范围.
恒成立,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在一次射击预选赛中,甲、乙两人各射击![]() 次,两人成绩的条形统计图如图所示,则下列四个选项中判断不正确的是( )
次,两人成绩的条形统计图如图所示,则下列四个选项中判断不正确的是( )

A. 甲的成绩的平均数小于乙的成绩的平均数
B. 甲的成绩的中位数小于乙的成绩的中位数
C. 甲的成绩的方差大于乙的成绩的方差
D. 甲的成绩的极差小于乙的成绩的极差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com