过点P(1,3)的动直线交圆C:x2+y2=4于A、B两点,分别过A、B作圆C的切线,如果两切线相交于点Q,那么点Q的轨迹为( )
A.直线的一部分
B.直线
C.圆的一部分
D.射线
【答案】
分析:根据圆的对称性可得Q点是经过C点垂直于AB的直线与A点切线的交点.由此设A(m,n),Q(x,y),根据圆的切线的性质与直线斜率公式,分别求出直线AQ、CQ方程,两个方程消去m、n得关于x、y的一次方程,即为点Q轨迹所在直线方程,再根据图形可得直线与圆C相交而Q不可能在圆上或圆内,可得Q轨迹是直线的一部分.
解答:解:
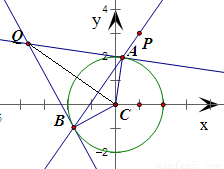
设A(m,n),Q(x,y),根据圆的对称性可得
Q点是经过C点垂直于AB的直线与A点切线的交点
∵圆x
2+y
2=4的圆心为C(0,0)
∴切线AQ的斜率为k
1=-
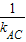
=-

,得
得AQ方程为y-n=-
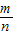
(x-m),化简得y=-
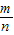
x+
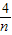
…①
又∵直线PA的斜率k
PA=
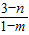
,
∴直线CQ的斜率k
2=-
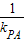
=
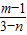
,
得直线CQ方程为y=
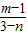
x…②
①②联解,消去m、n得x+3y-4=0,即为点Q轨迹所在直线方程
由于直线x+3y-4=0与圆C:x
2+y
2=4相交,所以直线位于圆上或圆内的点除外
故选:A
点评:本题给出定点P与圆C,求过P的圆的割线构成的两条切线的交点Q的轨迹.着重考查了圆的性质、直线的基本量与基本形式、直线与圆的位置关系等知识,属于中档题.

 设A(m,n),Q(x,y),根据圆的对称性可得
设A(m,n),Q(x,y),根据圆的对称性可得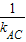 =-
=- ,得
,得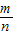 (x-m),化简得y=-
(x-m),化简得y=-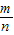 x+
x+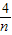 …①
…①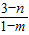 ,
,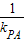 =
=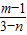 ,
,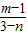 x…②
x…②

 阅读快车系列答案
阅读快车系列答案 (a>b>0)的左、右焦点分别为F1和F2,下顶点为A,直线AF1与椭圆的另一个交点为B,△ABF2的周长为8,直线AF1被圆O:x2+y2=b2截得的弦长为3.
(a>b>0)的左、右焦点分别为F1和F2,下顶点为A,直线AF1与椭圆的另一个交点为B,△ABF2的周长为8,直线AF1被圆O:x2+y2=b2截得的弦长为3.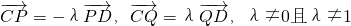 .求证:点Q总在某定直线上.
.求证:点Q总在某定直线上.