
分析 根据递推关系是求解得出$\frac{1}{{a}_{n+1}}$-1=$\frac{1}{2}$[$\frac{1}{{a}_{n}}$-1],运用等比数列定义$\frac{\frac{1}{{a}_{n+1}}-1}{\frac{1}{{a}_{n}}-1}$=$\frac{1}{2}$=常数.可判断求解.
解答 解:∵an+1=$\frac{2{a}_{n}}{{a}_{n+1}}$,a1=2,
∴$\frac{1}{{a}_{n+1}}$-1=$\frac{1}{2}$[$\frac{1}{{a}_{n}}$-1],$\frac{1}{{a}_{1}}$=$\frac{1}{2}-1$=$-\frac{1}{2}$,
∴$\frac{\frac{1}{{a}_{n+1}}-1}{\frac{1}{{a}_{n}}-1}$=$\frac{1}{2}$=常数.
{$\frac{1}{{a}_{n}}$-1}是以$-\frac{1}{2}$为首项,以$\frac{1}{2}$为公比的等比数列,
∴$\frac{1}{{a}_{n}}$-1=($-\frac{1}{2}$)×($\frac{1}{2}$)n-1=-($\frac{1}{2}$)n,
∴$\frac{1}{{a}_{n}}$=1-$\frac{1}{{2}^{n}}$
即an=$\frac{{2}^{n}}{{2}^{n}-1}$
点评 本题利用数列的递推关系是求解转化为等比数列求解通项公式,属于容易题,关键是恒等变形得出需要的条件.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|\overrightarrow a|=\sqrt{{{(\overrightarrow a)}^2}}$ | B. | λ($\overrightarrow a$•$\overrightarrow b$)=$\overrightarrow a$•(λ$\overrightarrow b$) | C. | ($\overrightarrow a$-$\overrightarrow b$)$\overrightarrow c$=$\overrightarrow a$•$\overrightarrow c$-$\overrightarrow b$•$\overrightarrow c$ | D. | $\overrightarrow a$与$\overrightarrow b$共线?$\overrightarrow a$•$\overrightarrow b$=$|{\overrightarrow a}||{\overrightarrow b}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
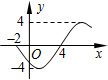 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com