
【题目】设函数f(x)=|x﹣ ![]() |+|x+m|(m>0)
|+|x+m|(m>0)
(1)证明:f(x)≥4;
(2)若f(2)>5,求m的取值范围.
【答案】
(1)
证明:由m>0,有f(x)=|x﹣ ![]() |+|x+m|≥|﹣(x﹣
|+|x+m|≥|﹣(x﹣ ![]() )+x+m|=
)+x+m|= ![]() +m≥4,
+m≥4,
当且仅当 ![]() =m,即m=2时取“=”,所以f(x)≥4成立.
=m,即m=2时取“=”,所以f(x)≥4成立.
(2)
解:f(2)=|2﹣ ![]() |+|2+m|.
|+|2+m|.
当 ![]() <2,即m>2时,f(2)=m﹣
<2,即m>2时,f(2)=m﹣ ![]() +4,由f(2)>5,求得m>
+4,由f(2)>5,求得m> ![]() .
.
当 ![]() ≥2,即0<m≤2时,f(2)=
≥2,即0<m≤2时,f(2)= ![]() +m,由f(2)>5,求得0<m<1.
+m,由f(2)>5,求得0<m<1.
综上,m的取值范围是(0,1)∪( ![]() ,+∞)
,+∞)
【解析】(1)由m>0,由f(x)的解析式利用绝对值三角不等式证得结论.(2)分当 ![]() <2时和当
<2时和当 ![]() ≥2时两种情况,分别根据f(2)>5,求得m的范围,再把所得m的范围取并集,即得所求.
≥2时两种情况,分别根据f(2)>5,求得m的范围,再把所得m的范围取并集,即得所求.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(2)商店记录了50天该商品的日需求量(单位:件),整理得表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间[400,550]”为事件A,求P(A)的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ ![]() x2﹣x+a(a∈R)在其定义域内有两个不同的极值点.
x2﹣x+a(a∈R)在其定义域内有两个不同的极值点.
(1)求a的取值范围;
(2)记两个极值点分别为x1 , x2 , 且x1<x2 . 已知λ>0,若不等式e1+λ<x1x2λ恒成立,求λ的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE长为30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足tan θ=![]() .
.

(1)若设计AB=18米,AD=6米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计AB与AD的长度,可使得活动中心的截面面积最大? (注:计算中π取3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .下列命题正确的为_______________.
.下列命题正确的为_______________.
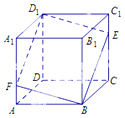
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() ,直线
,直线![]()
![]() ,过
,过![]() 的一条动直线
的一条动直线![]() 与直线
与直线![]() 相交于N,与圆C相交于P,Q两点,M是PQ中点.
相交于N,与圆C相交于P,Q两点,M是PQ中点.
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)设![]() ,试问
,试问![]() 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出![]() 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项为正的等比数列{an}的前n项和为Sn , S4=30,过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(﹣1,﹣1)
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn
,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ADCE中,AD∥EC,∠ADC=90°,AB⊥EC,AB=EB=1, ![]() .将△ABE沿AB折到△ABE1的位置,使∠BE1C=90°.M,N分别为BE1 , CD的中点.如图2.
.将△ABE沿AB折到△ABE1的位置,使∠BE1C=90°.M,N分别为BE1 , CD的中点.如图2. 
(1)求证:MN∥平面ADE1;
(2)求证:AM⊥E1C;
(3)求平面AE1N与平面BE1C所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com