
 ,共投篮5次.
,共投篮5次. ,故他他在投篮过程中至少投进1次的概率,利用互斥事件的概率公式,得:P=1-
,故他他在投篮过程中至少投进1次的概率,利用互斥事件的概率公式,得:P=1- =
= ;
; =
=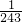 ,
,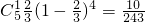 ,
, ,
,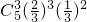 =
= ,
,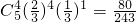 ,
, ,
, ,Dξ=5×
,Dξ=5× .
. ,共投篮5次,并且每次投篮相互之间互不影响,利用相互独立事件的概率公式即可求得;
,共投篮5次,并且每次投篮相互之间互不影响,利用相互独立事件的概率公式即可求得;

 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
一名学生骑自行车上学,从他的家到学校的途中有6个交通岗,假设他在各交通岗遇到红灯的事件是独立的,并且概率都是 ,
,
(1)求这名学生首次遇到红灯前,已经过了两个交通岗的概率.
(2)求这名学生在途中遇到红灯数 的期望与方差.
的期望与方差.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com