
分析 (1)由z2=-2i,展开后利用复数相等的条件求得a值;
(2)利用复数代数形式的乘除运算化简即可求得复平面内与$\frac{z}{1+i}$对应的点的坐标.
解答 解:(1)∵z2=(a-i)2=a2-1-2ai,
由题意,a2-1-2ai=-2i,
∴$\left\{{\begin{array}{l}{{a^2}-1=0}\\{-2a=-2}\end{array}}\right.$,解得a=1.
(2)由题意,z=2-i,
∴$\frac{z}{1+i}=\frac{2-i}{1+i}=\frac{(2-i)(1-i)}{(1+i)(1-i)}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i$,
∴复数$\frac{z}{1+i}$在复平面内所对应的点坐标为$(\frac{1}{2},-\frac{3}{2})$.
点评 本题考查复数代数形式的乘除运算,考查复数相等的条件,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | e3 | C. | 4 | D. | e4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知${a_n}=2n(n∈{N^*})$,把数列{an}的各项按如图的规律排成一个三角形数阵,记F(p,q)表示第p行从左至右的第q个数,则F(8,6)的值为110.
已知${a_n}=2n(n∈{N^*})$,把数列{an}的各项按如图的规律排成一个三角形数阵,记F(p,q)表示第p行从左至右的第q个数,则F(8,6)的值为110.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | B. | [kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$](k∈Z) | ||
| C. | [kπ-$\frac{2π}{3}$,kπ-$\frac{π}{6}$](k∈Z) | D. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
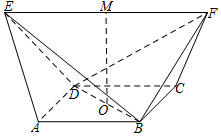 如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.
如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com