
【题目】上海地铁四通八达,给市民出行带来便利,已知某条线路运行时,地铁的发车时间间隔![]() (单位:分字)满足:
(单位:分字)满足:![]() ,
,![]() ,经测算,地铁载客量
,经测算,地铁载客量![]() 与发车时间间隔
与发车时间间隔![]() 满足
满足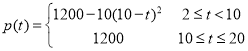 ,其中
,其中![]() .
.
(1)请你说明![]() 的实际意义;
的实际意义;
(2)若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?并求最大净收益.
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?并求最大净收益.
【答案】(1)发车间隔为5,载客量为950;(2)![]() ,
,![]() .
.
【解析】
(1)根据分段函数的表达式进行判断即可.
(2)求出Q的表达式,结合基本不等式以及函数单调性的性质进行求最值即可.
解:(1)由分段函数的表达式得p(5)的实际意义,发车间隔为5,载客量为950;
(2)当2≤x<10时,p(t)=﹣10t2+200t+200,
![]() 360=840﹣60(t
360=840﹣60(t![]() )≤840﹣60
)≤840﹣60![]() 840﹣60×12=120,当且仅当t
840﹣60×12=120,当且仅当t![]() ,即t=6时取等号.
,即t=6时取等号.
当10≤t≤20,![]() 360
360![]() 360
360![]() 360=384﹣360=24.
360=384﹣360=24.
则当t=6,Qmax=120.
即发车时间间隔为6分钟时,该线路每分钟的净收益最大,最大净收益为120元.


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)若不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数f(x)=![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,连接
,连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 时,求二面角
时,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样.
②某地气象局预报:5月9日本地降水概率为![]() ,结果这天没下雨,这表明天气预报并不科学.
,结果这天没下雨,这表明天气预报并不科学.
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.
④在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 增加0.1个单位.
增加0.1个单位.
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设实数![]() ,椭圆
,椭圆![]() 的右焦点为F,过F且斜率为k的直线交D于P、Q两点,若线段PQ的中点为N,点O是坐标原点,直线ON交直线
的右焦点为F,过F且斜率为k的直线交D于P、Q两点,若线段PQ的中点为N,点O是坐标原点,直线ON交直线![]() 于点M.
于点M.
![]() 若点P的横坐标为1,求点Q的横坐标;
若点P的横坐标为1,求点Q的横坐标;
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于数列![]() ,给出下列命题:①数列
,给出下列命题:①数列![]() 满足
满足![]() ,则数列
,则数列![]() 为公比为2的等比数列;②“
为公比为2的等比数列;②“![]() ,
,![]() 的等比中项为
的等比中项为![]() ”是“
”是“![]() ”的充分不必要条件:③数列
”的充分不必要条件:③数列![]() 是公比为
是公比为![]() 的等比数列,则其前
的等比数列,则其前![]() 项和
项和![]() ;④等比数列
;④等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ,
,![]() ,
,![]() 成等比数列,其中假命题的序号是( )
成等比数列,其中假命题的序号是( )
A.②B.②④C.①②④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com