
(12分)如图所示,以AB=4 cm,BC=3 cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5 cm,BF=8 cm,CG=12 cm时,试回答下列问题:
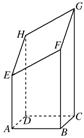
(1)求DH的长;
(2)求这个几何体的体积;
(3)截面四边形EFGH是什么图形?证明你的结论.
解:(1)过E作EB1⊥BF,垂足为B1,则BB1=AE=5(cm),
所以B1F=8-5=3(cm).
因为平面ABFE∥平面DCGH,EF和HG是它们分别与截面的交线,所以EF∥HG.
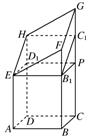
过H作HC1⊥CG,垂足为C1,
则GC1=FB1=3(cm),
DH=12-3=9(cm). ----------------------------------- 4分
(2)作ED1⊥DH,垂足为D1,B1P⊥CG,垂足为P,连结D1P,B1C1,则几何体被分割成一个长方体ABCD-EB1PD1,一个斜三棱柱EFB1-HGC1,一个直三棱柱EHD1-B1C1P.从而几何体的体积为
V=3×4×5+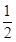 ×3×4×3+
×3×4×3+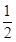 ×3×4×4=102(cm3).--------------8分
×3×4×4=102(cm3).--------------8分
(3)是菱形.
证明:由(1)知EF∥HG,同理EH∥FG.于是EFGH是平行四边形.
因为EF=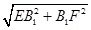 =
=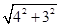
=5(cm),
DD1=AE=5(cm),ED1=AD=3(cm),
HD1=4(cm),
所以EH=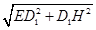 =
=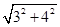
=5(cm).
所以EF=EH.
故EFGH是菱形. ------------------------------------------12分
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年甘肃省河西五市高三第一次联合考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形, BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.

(1)证明:平面PBE 平面PAB;
平面PAB;
(2)求PC与平面PAB所成角的余弦值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年云南玉溪一中高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本题满分12分)
如图所示,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.

(1)证明:PQ⊥平面DCQ;
(2)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省岳阳市高三第一次质量检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图所示多面体中, ⊥平面
⊥平面 ,
, 为平行四边形,
为平行四边形, 分别为
分别为 的中点,
的中点, ,
, ,
,
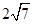 .
.
(1)求证: ∥平面
∥平面 ;
;
(2)若∠ =90°,求证
=90°,求证 ;
;
(3)若∠ =120°,求该多面体的体积.
=120°,求该多面体的体积.

查看答案和解析>>
科目:高中数学 来源:2011年山东省青岛市高考模拟练习题(一)数学(理) 题型:解答题
(本小题满分12分)如图所示的几何体是由以等边三角形 为底面的棱柱被平面
为底面的棱柱被平面 所截而得,已知
所截而得,已知 平面
平面 ,
, ,
, ,
, ,
,  为
为 的中点,
的中点, 面
面 .
.
(Ⅰ)求 的长;
的长;
(Ⅱ)求证:面 面
面 ;
;
(Ⅲ)求平面 与平面
与平面 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省中山市高三第一次月考数学理卷 题型:解答题
(本小题满分12分)如图所示,在正方体 中,
中,
E为AB的中点
(1)若 为
为 的中点,求证:
的中点,求证: 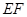 ∥面
∥面 ;
;
(2) 若 为
为 的中点,求二面角
的中点,求二面角 的余弦值;
的余弦值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com