
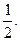 点
点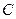 在
在 轴上,
轴上,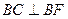 ,且
,且 、
、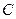 、
、 三点确定的圆
三点确定的圆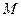 恰好与直线
恰好与直线 相切.
相切. 作一条与两坐标轴都不垂直的直线
作一条与两坐标轴都不垂直的直线 交椭圆于
交椭圆于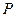 、
、 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 恰好为△
恰好为△ 的内角平分线,若存在,求出点
的内角平分线,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
科目:高中数学 来源:不详 题型:解答题
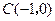 及椭圆
及椭圆 ,过点
,过点 的动直线与椭圆相交于
的动直线与椭圆相交于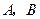 两点.
两点. 中点的横坐标是
中点的横坐标是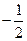 ,求直线
,求直线 的方程;
的方程; 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
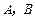 两点相距2千米,现准备在荒漠上围垦出一片以
两点相距2千米,现准备在荒漠上围垦出一片以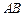 为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.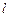 刚好通过点
刚好通过点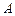 ,且
,且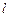 与
与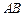 成
成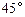 角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
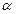 (
(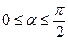 )方向行走一段时间后,再向正北方向行走一段时间,但何时改变方向不定。假定机器人行走速度为10米/分钟,则机器人行走2分钟时的可能落点区域的面积是 。
)方向行走一段时间后,再向正北方向行走一段时间,但何时改变方向不定。假定机器人行走速度为10米/分钟,则机器人行走2分钟时的可能落点区域的面积是 。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
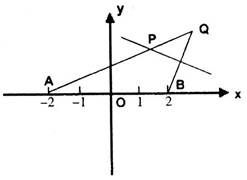
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com