
【题目】如图(1),边长为![]() 的正方形
的正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,现沿
,现沿![]() 把
把![]() 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将![]() ,
,![]() ,
,![]() 沿
沿![]() ,
,![]() ,
,![]() 折起,使
折起,使![]() 、
、![]() 、
、![]() 三点重合于点
三点重合于点![]() ,如图(3).
,如图(3).
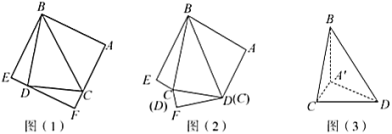
(1)求证:![]() ;
;
(2)求二面角![]() 最小时的余弦值.
最小时的余弦值.
科目:高中数学 来源: 题型:
【题目】某篮球教练对甲乙两位运动员在近五场比赛中的得分情况统计如下图所示,根据图表给出如下结论:(1)甲乙两人得分的平均数相等且甲的方差比乙的方差小;(2)甲乙两人得分的平均数相等且甲的方差比乙的方差大;(3)甲的成绩在不断提高,而乙的成绩无明显提高;(4)甲的成绩较稳定,乙的成续基本呈上升状态;结论正确的是( )
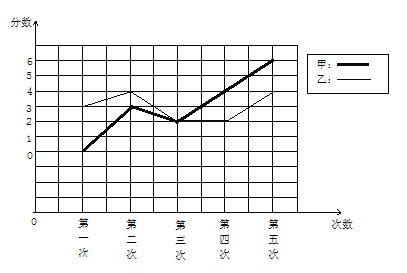
A.(1)(3)B.(1)(4)C.(2)(3)D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)在曲线![]() 上是否存在点P,使得过点P可作三条直线与曲线
上是否存在点P,使得过点P可作三条直线与曲线![]() 相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织了垃圾分类知识竞赛活动.设置了四个箱子,分别写有“厨余垃圾”、“有害垃圾”、“可回收物”、“其它垃圾”;另有卡片若干张,每张卡片上写有一种垃圾的名称.每位参赛选手从所有卡片中随机抽取![]() 张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得
张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得![]() 分,投放错误得
分,投放错误得![]() 分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得
分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得![]() 分,放入其它箱子,得
分,放入其它箱子,得![]() 分.从所有参赛选手中随机抽取
分.从所有参赛选手中随机抽取![]() 人,将他们的得分按照
人,将他们的得分按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如图:
分组,绘成频率分布直方图如图:
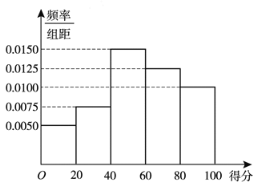
(1)分别求出所抽取的![]() 人中得分落在组
人中得分落在组![]() 和
和![]() 内的人数;
内的人数;
(2)从所抽取的![]() 人中得分落在组
人中得分落在组![]() 的选手中随机选取
的选手中随机选取![]() 名选手,以
名选手,以![]() 表示这
表示这![]() 名选手中得分不超过
名选手中得分不超过![]() 分的人数,求
分的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3) 如果某选手将抽到的20张卡片逐一随机放入四个箱子,能否认为该选手不会得到100分?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于工作需要,某公司准备一次性购买两台具有智能打印、扫描、复印等多种功能的智能激光型打印机.针对购买后未来五年内的售后,厂家提供如下两种方案:
方案一:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元;
元;
方案二:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元.
元.
该公司搜集并整理了![]() 台这款打印机使用五年的维修次数,所得数据如下表所示:
台这款打印机使用五年的维修次数,所得数据如下表所示:
维修次数 |
|
|
|
|
台数 |
|
|
|
|
以这![]() 台打印机使用五年的维修次数的频率代替
台打印机使用五年的维修次数的频率代替![]() 台打印机使用五年的维修次数的概率,记
台打印机使用五年的维修次数的概率,记![]() 表示这两台智能打印机五年内共需维修的次数.
表示这两台智能打印机五年内共需维修的次数.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以两种方案产生的维修费用的期望值为决策依据,写出你的选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商贸公司售卖某种水果.经市场调研可知:在未来![]() 天内,这种水果每箱的销售利润
天内,这种水果每箱的销售利润![]() (单位:元)与时间
(单位:元)与时间![]() ,单位:天)之间的函数关系式为
,单位:天)之间的函数关系式为![]() , 且日销售量
, 且日销售量![]() (单位:箱)与时间
(单位:箱)与时间![]() 之间的函数关系式为
之间的函数关系式为![]()
①第![]() 天的销售利润为__________元;
天的销售利润为__________元;
②在未来的这![]() 天中,公司决定每销售
天中,公司决定每销售![]() 箱该水果就捐赠
箱该水果就捐赠![]() 元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间
元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间![]() 的增大而增大,则
的增大而增大,则![]() 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像过点
的图像过点![]() 和
和![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的最小值;
的最小值;
(3)记![]() ,
,![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com