【题目】衣橱中有5件上衣，其中2件蓝色、3件白色，有8条裤子，其中3条蓝色、5条黑色．则随机取一件上衣和一条裤子，上衣与裤子同色的概率为________，上衣和裤子中至少有一个为蓝色的概率为_________．
科目：高中数学 来源： 题型：
【题目】已知梯形ABCD满足AB∥CD，∠BAD＝45°，以A，D为焦点的双曲线Γ经过B，C两点.若CD＝7AB，则双曲线Γ的离心率为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系，随机调查了某中学高三某班
名学生每周课下钻研数学时间
(单位：小时)与高三下学期期中考试数学解答题得分
，数据如下表：
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
（1）根据上述数据，求出数学考试中的解答题得分与该学生课下钻研数学时间的线性回归方程，并预测某学生每周课下钻研数学时间为
小时其数学考试中的解答题得分；
（2）从这人中任选
人，求人中至少有
人课下钻研数学时间不低于
小时的概率.
参考公式：
，其中
，
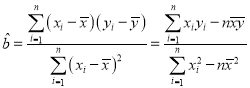；参考数据：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某运输公司每天至少向某地运送
物质，该公司有8辆载重为
的
型卡车与4辆载重为
的
型卡车，有10名驾驶员，每辆卡车每天往返的次数为型卡车4次，型卡车3次；每辆卡车每天往返的成本为型卡车320元，型卡车504元，你认为该公司怎样调配车辆，使运费成本最低，最低运费是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两人各射击一次，击中目标的概率分别是
和
，假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响．
（1）求甲射击4次，至多1次未击中目标的概率；
（2）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
（3）假设某人连续2次未击中目标，则停止射击，求乙恰好射击5次后被中止射击的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】 在平行四边形ABCD中，A(1，1)，
＝(6，0)，点M是线段AB的中点，线段CM与BD交于点P．(1) 若
＝(3，5)，求点C的坐标；(2) 当||＝||时，求点P的轨迹．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】A，B两组各有7位病人，他们服用某种药物后的康复时间（单位：天）记录如下：
A组：10，11，12，13，14，15，16；
B组：12，13，15，16，17，14，
.
假设所有病人的康复时间相互独立，从A，B两组随机各选1人，A组选出的人记为甲，B组选出的人记为乙.
（1）求甲的康复时间不少于14天的概率；
（2）如果
，求甲的康复时间比乙的康复时间长的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
