
【题目】如图,在直三棱柱ABCA1B1C1中,D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD-A1B1C1的体积.
科目:高中数学 来源: 题型:
【题目】 在平行四边形ABCD中,A(1,1),![]() =(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若![]() =(3,5),求点C的坐标;(2) 当|
=(3,5),求点C的坐标;(2) 当|![]() |=|
|=|![]() |时,求点P的轨迹.
|时,求点P的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两同学利用暑假到某县进行社会实践,对该县的养鸡场连续六年来的规模进行调查研究,得到如下两个不同的信息图:
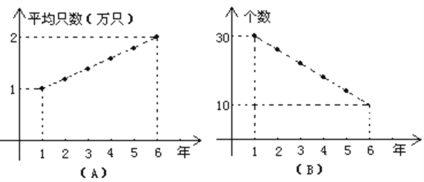
(A)图表明:从第1年平均每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡:
(B)图表明:由第1年养鸡场个数30个减少到第6年的10个.
请你根据提供的信息解答下列问题:
(1)第二年的养鸡场的个数及全县出产鸡的总只数各是多少?
(2)哪一年的规模最大?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本C(x),当年产量不足80千件时,C(x)= ![]() x2+10x(万元);当年产量不小于80千件时C(x)=51x+
x2+10x(万元);当年产量不小于80千件时C(x)=51x+ ![]() ﹣1450(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
﹣1450(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足:对任意x,y∈R,都有f(x+y)=f(x)f(y)﹣f(x)﹣f(y)+2成立,且x>0时,f(x)>2,
(1)求f(0)的值,并证明:当x<0时,1<f(x)<2.
(2)判断f(x)的单调性并加以证明.
(3)若函数g(x)=|f(x)﹣k|在(﹣∞,0)上递减,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且Sn=n2﹣4n﹣5
(1)求数列{an}的通项公式;
(2)设bn=|an|,数列{bn}的前n项和为Tn, 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取![]() 名学生的身高,将数据整理,得到的频率分布表如下所示,
名学生的身高,将数据整理,得到的频率分布表如下所示,
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| 0.350 | |
第3组 |
| 30 | |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 |
| 1.00 | |
(Ⅰ)求出频率分布表中①和②位置上相应的数据,并完成下列频率分布直方图;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样抽取6名学生进行不同项目的体能测试,若在这6名学生中随机抽取2名学生进行引体向上测试,则第4组中至少有一名学生被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com