练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在锐角△ABC中，已知a、b、c分别是三内角A、B、C所对应的边长，且b=2asinB．
    （1）求角A的大小；
    （2）若b=1，且△ABC的面积为，求a的值．

    （1）（2）

    解析试题分析：（1）根据正弦定理可直接推倒得出。（2）由面积公式可得边的长，用余弦定理可得边长。
    试题解析：解：由及正弦定理得       3分
    又为锐角，所以    6分
    （2）由△ABC的面积为得
       8分
    又 ，，∴    11分
    由余弦定理得
    ∴   14分
    考点：1正弦定理；2余弦定理。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某人在汽车站M的北偏西20°的方向上的A处(如图所示)，观察到C处有一辆汽车沿公路向M站行驶，公路的走向是M站的北偏东40°.开始时，汽车到A处的距离为31km，汽车前进20km后，到A处的距离缩短了10km.问汽车还需行驶多远，才能到达汽车站M?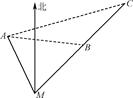

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，角A，B，C的对边分别为a，b，c，若acos2＋ccos2＝b.
    (1)求证：a，b，c成等差数列；
    (2)若∠B＝60°，b＝4，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，已知＝3.
    (1)求证：tan B＝3tan A；
    (2)若cos C＝，求A的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知向量记.
    （1）若，求的值；
    （2）在△ABC中，角A、B、C的对边分别是、、，且满足，若，试判断△ABC的形状.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在中，角、、对的边分别为、、，且
    （1）求的值；
    （2）若，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△中，三个内角，，的对边分别为，，，=(b,a),=(cosB,sinA)，且||（Ⅰ）求角；（Ⅱ）若，c=2a， 求△的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知△ABC的内角为A、B、C，其对边分别为a、b、c，B为锐角，向量m＝(2sin B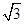，－)，n＝，且m∥n
    (1)求角B的大小；
    (2)如果b＝2，求S△ABC的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，在△ABC中，∠ABC＝90°，AB＝，BC＝1，P为△ABC内一点，∠BPC＝90°.

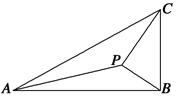
    (1)若PB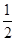＝，求PA；
    (2)若∠APB＝150°，求tan∠PBA.

    查看答案和解析>>

    同步练习册答案