
分析 设M(x,y),得出B(x,-3),化简$\overrightarrow{MA}•\overrightarrow{AB}=\overrightarrow{MB}•\overrightarrow{BA}$,列方程化简即可.
解答 解:设M(x,y),∵$\overrightarrow{MB}∥\overrightarrow{OA}$,Bz在直线y=-3上,∴B(x,-3).
∴$\overrightarrow{MA}$=(-x,-1-y),$\overrightarrow{MB}$=(0,-3-y),$\overrightarrow{AB}$=(x,-2).
∵$\overrightarrow{MA}•\overrightarrow{AB}=\overrightarrow{MB}•\overrightarrow{BA}$,∴$\overrightarrow{MA}•\overrightarrow{AB}$+$\overrightarrow{MB}•\overrightarrow{AB}$=0,即($\overrightarrow{MA}+\overrightarrow{MB}$)•$\overrightarrow{AB}$=0,
∵$\overrightarrow{MA}+\overrightarrow{MB}$=(-x,-4-2y),
∴($\overrightarrow{MA}+\overrightarrow{MB}$)$•\overrightarrow{AB}$=-x2+2(4+2y)=0,
化简得:$y=\frac{1}{4}{x^2}-2$.
∴M点的轨迹方程为y=$\frac{1}{4}$x2-2.
点评 本题考查了平面向量的数量积运算,轨迹方程的求解,属于中档题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:2015-2016学年陕西省高一下学期期末考数学试卷(解析版) 题型:解答题
已知函数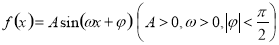 的图像过点
的图像过点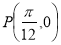 ,图像上与
,图像上与
点P最近的一个顶点是
(1)求函数的解析式;
(2)求使函数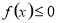 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
已知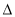 ABC的三边为a,b,c.其面积S=
ABC的三边为a,b,c.其面积S= 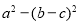 ,且b+c=8.
,且b+c=8.
(1)求cosA
(2)求S的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
设数列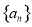 的前
的前 项和为
项和为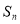 ,且
,且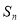
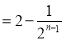 ,
,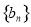 为等差数列,且
为等差数列,且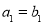 ,
,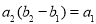 .
.
(1)求数列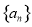 和
和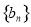 通项公式;
通项公式;
(2)设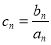 ,求数列
,求数列 的前
的前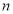 项和
项和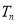 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{\sqrt{6}}{3}$),($\frac{\sqrt{6}}{3}$,+∞) | B. | (-$\sqrt{2}$,-$\frac{\sqrt{6}}{3}$),($\sqrt{2}$,+∞) | C. | (-$\sqrt{2}$,-$\frac{\sqrt{6}}{3}$),($\frac{\sqrt{6}}{3}$,+∞) | D. | (-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{18}-\frac{y^2}{32}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{25}=1$ | D. | $\frac{x^2}{36}-\frac{y^2}{64}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com