
【题目】已知函数![]() (其中
(其中![]() 为常数).
为常数).
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)若不等式![]() 在
在![]() 时有解,求实数
时有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,是否存在正数
,是否存在正数![]() ,使得对于区间
,使得对于区间![]() 上的任意三个实数
上的任意三个实数![]() ,
,![]() ,
,![]() ,都存在以
,都存在以![]() ,
,![]() ,
,![]() 为边长的三角形?若存在,试求出这样的
为边长的三角形?若存在,试求出这样的![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ,偶函数;
,偶函数; ![]() ,非奇非偶函数;(2)
,非奇非偶函数;(2)![]() ;(3)
;(3) .
.
【解析】
(1)先由题意得到函数![]() 的定义域,再由函数奇偶性的定义,分别讨论
的定义域,再由函数奇偶性的定义,分别讨论![]() 与
与![]() ,即可判断出结果;
,即可判断出结果;
(2)先由题意,将问题转化为![]() 在
在![]() 上能成立;求出
上能成立;求出![]() 的最大值,即可得出结果;
的最大值,即可得出结果;
(3)先假设存在正数![]() 满足题意;设
满足题意;设![]() ,求出
,求出![]() ,将对于区间
,将对于区间![]() 上的任意三个实数
上的任意三个实数![]() ,
,![]() ,
,![]() ,都存在以
,都存在以![]() ,
,![]() ,
,![]() 为边长的三角形,转化为
为边长的三角形,转化为![]() ,任取
,任取![]() ,作差得到
,作差得到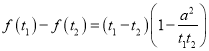 ,分别讨论
,分别讨论![]() ,
,![]() ,
,![]() ,
,![]() 四种情况,得出函数单调性,求出最值,列出不等式求解,即可得出结果.
四种情况,得出函数单调性,求出最值,列出不等式求解,即可得出结果.
(1)由题意可得:![]() 的定义域为
的定义域为![]() ,
,
又![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 是偶函数;
是偶函数;
当![]() ,即
,即![]() 时,
时,![]() 是非奇非偶函数;
是非奇非偶函数;
(2)由不等式![]() 可得:
可得:![]() ,即
,即![]() ,
,
所以不等式![]() 在
在![]() 时有解,
时有解,
等价于![]() 在
在![]() 上能成立;
上能成立;
又![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]()
因此,只需![]() ,解得
,解得![]() ;
;
即实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)假设存在正数![]() 满足题意;
满足题意;
设![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,则
,则![]() ;
;
所以对于区间![]() 上的任意三个实数
上的任意三个实数![]() ,
,![]() ,
,![]() ,都存在以
,都存在以![]() ,
,![]() ,
,![]() 为边长的三角形,等价于
为边长的三角形,等价于![]() ,
,
任取![]() ,所以
,所以![]() ,
,![]()
则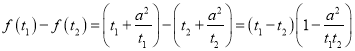 ,
,
①当![]() 时,
时,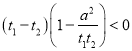 ,所以
,所以![]() ,
,
即![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,![]() ,
,
由![]() 得
得![]() ,解得:
,解得:![]() ,所以
,所以![]() ;
;
②当![]() 时,易得:
时,易得:![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
![]() ,
,
由![]() 得:
得:![]() ,解得:
,解得:![]() ;
;
所以![]() ;
;
③当![]() 时,易得:
时,易得:![]() 在在
在在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
![]() ,
,
由![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
所以![]() ;
;
④当![]() 时,
时, ,所以
,所以![]() ,
,
即![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
综上,![]() ,又
,又![]() 为正数,所以
为正数,所以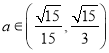 .
.
即存在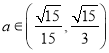 满足题意.
满足题意.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2ωxcosφ+cos2ωxsinφ+
sin2ωxcosφ+cos2ωxsinφ+ ![]() cos(
cos( ![]() +φ)(0<φ<π),其图象上相邻两条对称轴之间的距离为π,且过点(
+φ)(0<φ<π),其图象上相邻两条对称轴之间的距离为π,且过点( ![]() ). (I)求ω和φ的值;
). (I)求ω和φ的值;
(II)求函数y=f(2x),x∈[0, ![]() ]的值域.
]的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司现提供两种一年期投资理财方案,一年后投资盈亏的情况如表:
投资股市 | 获利40% | 不赔不赚 | 亏损20% | 购买基金 | 获利20% | 不赔不赚 | 亏损10% |
概率P | | | | 概率P | p | | q |
(I)甲、乙两人在投资顾问的建议下分别选择“投资股市”和“购买基金”,若一年后他们中至少有一人盈利的概率大于 ![]() ,求p的取值范围;
,求p的取值范围;
(II)某人现有10万元资金,决定在“投资股市”和“购买基金”这两种方案中选出一种,若购买基金现阶段分析出 ![]() ,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  ,g(x)=af(x)﹣|x﹣1|.
,g(x)=af(x)﹣|x﹣1|.
(Ⅰ)当a=0时,若g(x)≤|x﹣2|+b对任意x∈(0,+∞)恒成立,求实数b的取值范围;
(Ⅱ)当a=1时,求g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+1,数列{an}满足an=f(n)(n∈N*),数列{bn}的前n项和为Tn , 且b1=2,Tn=bn+1﹣2(n∈N).
(1)分别求{an},{bn}的通项公式;
(2)定义x=[x]+(x),[x]为实数x的整数部分,(x)为小数部分,且0≤(x)<1.记cn= ![]() ,求数列{cn}的前n项和Sn .
,求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对一切实数x、y,不等式 ![]() ﹣cos2x≥asinx﹣
﹣cos2x≥asinx﹣ ![]() 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.(﹣∞, ![]() ]
]
B.[3,+∞)
C.[﹣2 ![]() ,2
,2 ![]() ]
]
D.[﹣3,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|+|x﹣2|,不等式f(x)≥t对x∈R恒成立.
(1)求t的取值范围;
(2)记t的最大值为T,若正实数a,b满足a2+b2=T,求证: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,过椭圆 ![]() 右焦点的直线
右焦点的直线 ![]() 交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为
交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设另一直线l与椭圆C交于A,B两点,原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,已知O为坐标原点,点A、B的坐标分别为(1,1)、(﹣3,3).若动点P满足 ![]() ,其中λ、μ∈R,且λ+μ=1,则点P的轨迹方程为( )
,其中λ、μ∈R,且λ+μ=1,则点P的轨迹方程为( )
A.x﹣y=0
B.x+y=0
C.x+2y﹣3=0
D.(x+1)2+(y﹣2)2=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com