
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点,
的中点,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的大小为45°,求直线
的大小为45°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明![]() ,
,![]() 得到答案.
得到答案.
(2)以与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,面
轴建立空间直角坐标系,面![]() 的法向量记为
的法向量记为![]() ,面
,面![]() 的法向量为
的法向量为![]() ,根据夹角得到
,根据夹角得到![]() ,平面
,平面![]() 的法向量
的法向量![]() ,计算得到答案.
,计算得到答案.
(1)因为点![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
所以四边形![]() 为平行四边形,即
为平行四边形,即![]() .
.
因为![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点,
的中点,![]() .
.
![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)如图所示

因为![]() ,
,![]() ,
,![]() 与
与![]() 为相交直线,所以
为相交直线,所以![]() 平面
平面![]() ,不妨设
,不妨设![]() ,则
,则![]() .
.
以与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,
面![]() 的法向量记为
的法向量记为![]() ,则
,则 ,可得
,可得 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
又面![]() 的法向量为
的法向量为![]() ,二面角
,二面角![]() 的大小为45°.
的大小为45°.
 ,解得
,解得![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,可得:
,可得: .
.
令![]() ,则
,则![]() ,
,![]() .所以
.所以![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则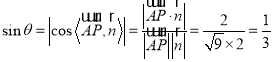 .
.


科目:高中数学 来源: 题型:
【题目】在如图所示的四棱锥![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,![]() 为边长为2的等边三角形,
为边长为2的等边三角形,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 是异面直线
是异面直线![]() 和
和![]() 的公垂线.
的公垂线.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)记![]() 的重心为
的重心为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试,根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间![]() 的左侧,则认为该学生属“体能不达标的学生,其中
的左侧,则认为该学生属“体能不达标的学生,其中![]() 分别为样本平均数和样本标准差,计算可得
分别为样本平均数和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).

(1)若该校高三某男生的跳远距离为![]() ,试判断该男生是否属于“体能不达标”的学生?
,试判断该男生是否属于“体能不达标”的学生?
(2)该校利用分层抽样的方法从样本区间![]() 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在
中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com