
【题目】下列函数中,同时满足两个条件“①x∈R,f( ![]() +X)+f(
+X)+f( ![]() -X)=0;②当﹣
-X)=0;②当﹣ ![]() <x<
<x< ![]() 时,f′(x)>0”的一个函数是( )
时,f′(x)>0”的一个函数是( )
A.f(x)=sin(2x+ ![]() )
)
B.f(x)=cos(2x+ ![]() )
)
C.f(x)=sin(2x﹣ ![]() )
)
D.f(x)=cos(2x﹣ ![]() )
)
科目:高中数学 来源: 题型:
【题目】![]() 已知数列
已知数列![]() 是递增的等比数列,a1+a4=9,a2a3=8,则数列
是递增的等比数列,a1+a4=9,a2a3=8,则数列![]() 的前n项和等于
的前n项和等于![]() ,解得a1=1,a4=8,或者a1=8,a4=1,但由于是递增数列,即a1=1,a4=8,即q3=
,解得a1=1,a4=8,或者a1=8,a4=1,但由于是递增数列,即a1=1,a4=8,即q3=![]() =8,所以q=2.因而数列
=8,所以q=2.因而数列![]() 的前n项和为 。
的前n项和为 。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+ ![]() }是等比数列,并求{an}的通项公式;
}是等比数列,并求{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,且过点
,且过点 ![]() ,直线l1:y=kx+m(m>0)与圆C2:(x﹣1)2+y2=1相切且与椭圆C1交于A,B两点. (Ⅰ)求椭圆C1的方程;
,直线l1:y=kx+m(m>0)与圆C2:(x﹣1)2+y2=1相切且与椭圆C1交于A,B两点. (Ⅰ)求椭圆C1的方程;
(Ⅱ)过原点O作l1的平行线l2交椭圆于C,D两点,设|AB|=λ|CD|,求λ的最小值.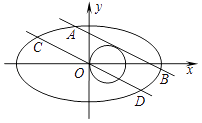
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两个容器,甲容器容量为x,装满纯酒精,乙容器容量为z,其中装有体积为y的水(x,y<z,单位:L).现将甲容器中的液体倒入乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒入甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过n(n∈N*)次操作之后,乙容器中含有纯酒精an(单位:L),下列关于数,列{an}的说法正确的是( )
A.当x=y=a时,数列{an}有最大值 ![]()
B.设bn=an+1﹣an(n∈N*),则数列{bn}为递减数列
C.对任意的n∈N* , 始终有 ![]()
D.对任意的n∈N* , 都有 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为非负整数的数列{an}同时满足下列条件: ①a1=m(m∈N*);②an≤n﹣1(n≥2);③n是a1+a2+…+an的因数(n≥1).
(Ⅰ)当m=5时,写出数列{an}的前五项;
(Ⅱ)若数列{an}的前三项互不相等,且n≥3时,an为常数,求m的值;
(Ⅲ)求证:对任意正整数m,存在正整数M,使得n≥M时,an为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,过椭圆M: ![]() =1(a>b>0)焦点的直线x+y﹣2
=1(a>b>0)焦点的直线x+y﹣2 ![]() =0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
=0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
(1)求M的方程;
(2)A、B是M的左、右顶点,C、D是M上的两点,若AC⊥BD,求四边形ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com