
【题目】已知函数f(x)=lnx﹣a(x﹣1),a∈R
(1)讨论函数f(x)的单调性;
(2)当x≥1时,f(x)≤ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】
(1)
解: f(x)的定义域为(0,+∞), ![]() ,
,
若a≤0,则f′(x)>0,∴f(x)在(0,+∞)上单调递增,
若a>0,则由f′(x)=0,得x= ![]() ,
,
当x∈(0, ![]() )时,f′(x)>0,
)时,f′(x)>0,
当x∈( ![]() )时,f′(x)<0,
)时,f′(x)<0,
∴f(x)在(0, ![]() )上单调递增,在(
)上单调递增,在( ![]() ,+∞)单调递减.
,+∞)单调递减.
所以当a≤0时,f(x)在(0,+∞)上单调递增,
当a>0时,f(x)在(0, ![]() )上单调递增,在(
)上单调递增,在( ![]() ,+∞)单调递减.
,+∞)单调递减.
(2)
解:f(x)﹣ ![]() =
= ![]() ,
,
令g(x)=xlnx﹣a(x2﹣1),(x≥1),
g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax,
![]() ,
,
①若a≤0,F′(x)>0,g′(x)在[1,+∞)递增,
g′(x)≥g′(1)=1﹣2a>0,
∴g(x)在[1,+∞)递增,g(x)≥g(1)=0,
从而f(x)﹣ ![]() 不符合题意.
不符合题意.
②若0<a< ![]() ,当x∈(1,
,当x∈(1, ![]() ),F′(x)>0,
),F′(x)>0,
∴g′(x)在(1, ![]() )递增,
)递增,
从而g′(x)>g′(1)=1﹣2a,
∴g(x)在[1,+∞)递增,g(x)≥g(1)=0,
从而f(x)﹣ ![]() 不符合题意.
不符合题意.
③若a ![]() ,F′(x)≤0在[1,+∞)恒成立,
,F′(x)≤0在[1,+∞)恒成立,
∴g′(x)在[1,+∞)递减,g′(x)≤g′(1)=1﹣2a≤0,
从而g9x)在[1,+∞)递减,
∴g(x)≤g(1)=0,f(x)﹣ ![]() ≤0,
≤0,
综上所述,a的取值范围是[ ![]() ).
).
【解析】(1)f(x)的定义域为(0,+∞), ![]() ,若a≤0,f(x)在(0,+∞)上单调递增;若a>0时,f(x)在(0,
,若a≤0,f(x)在(0,+∞)上单调递增;若a>0时,f(x)在(0, ![]() )上单调递增,在(
)上单调递增,在( ![]() ,+∞)单调递减.(2)f(x)﹣
,+∞)单调递减.(2)f(x)﹣ ![]() =
= ![]() ,令g(x)=xlnx﹣a(x2﹣1),(x≥1),g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax,
,令g(x)=xlnx﹣a(x2﹣1),(x≥1),g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax, ![]() ,由此进行分类讨论,能求出实数a的取值范围.
,由此进行分类讨论,能求出实数a的取值范围.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数有( )
①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差;反之,则越好;
越大时,模型的拟合效果越差;反之,则越好;
②可导函数![]() 在
在![]() 处取得极值,则
处取得极值,则![]() ;
;
③归纳推理是由特殊到一般的推理,而演绎推理是由一般到特殊的推理;
④综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1曰8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值![]() 与这种新材料的含量
与这种新材料的含量![]() (单位:克)的关系为:当
(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得数据如表(部分)
.测得数据如表(部分)
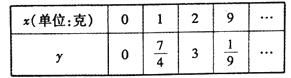
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)其函数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的参数方程为 ![]() (为参数,且0≤<2π),曲线l的极坐标方程为ρ=
(为参数,且0≤<2π),曲线l的极坐标方程为ρ= ![]() (k是常数,且k∈R).
(k是常数,且k∈R).
(1)求曲线C的普通方程和曲线l直角坐标方程;
(2)若曲线l被曲线C截的弦是以( ![]() ,1)为中点,求k的值.
,1)为中点,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 及函数
及函数![]() (a,b,c∈R),若a>b>c且a+b+c=0.
(a,b,c∈R),若a>b>c且a+b+c=0.
(1)证明:f(x)的图像与g(x)的图像一定有两个交点;
(2)请用反证法证明:![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知, ![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
参考公式:回归直线方程: ![]() .其中
.其中
(注: ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com