练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体中，点是棱上的一个动点，平面交棱于点．下列命题正确的为_______________.

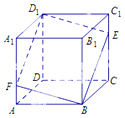
    ①存在点，使得//平面；

    ②对于任意的点，平面平面；

    ③存在点，使得平面；

    ④对于任意的点，四棱锥的体积均不变．

    【答案】①②④

    【解析】

    根据线面平行和线面垂直的判定定理，以及面面垂直的判定定理和性质分别进行判断即可．

    ①当为棱上的一中点时，此时也为棱上的一个中点，此时//，满足//平面，故①正确；

    ②连结，则平面，因为平面，所以平面平面，故②正确；

    ③平面，不可能存在点，使得平面，故③错误；

    ④四棱锥的体积等于，设正方体的棱长为1.

    ∵无论、在何点，三角形的面积为为定值，三棱锥的高，保持不变，三角形的面积为为定值，三棱锥的高为，保持不变.

    ∴四棱锥的体积为定值，故④正确.

    故答案为①②④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲，乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于100为优品，大于等于90且小于100为合格品，小于90为次品，现随机抽取这两台车床生产的零件各100件进行检测，检测结果统计如下：

    测试指标

    机床甲

    8

    12

    40

    32

    8

    机床乙

    7

    18

    40

    29

    6

    （1）试分别估计甲机床、乙机床生产的零件为优品的概率；

    （2）甲机床生产一件零件，若是优品可盈利160元，合格品可盈利100元，次品则亏损20元；假设甲机床某天生产50件零件，请估计甲机床该天的日利润（单位：元）；

    （3）从甲、乙机床生产的零件指标在内的零件中，采用分层抽样的方法抽取5件，从这5件中任选2件进行质量分析，求这2件都是乙机床生产的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知长方体AC1中，AD=AB=2，AA1=1，E为D1C1的中点，如图所示．

    （Ⅰ）在所给图中画出平面ABD1与平面B1EC的交线（不必说明理由）；
    （Ⅱ）证明：BD1∥平面B1EC；
    （Ⅲ）求平面ABD1与平面B1EC所成锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f′（x）是奇函数f（x）（x∈R）的导函数，f（﹣1）=0，当x＞0时，xf′（x）﹣f（x）＜0，则使得f（x）＞0成立的x的取值范围是（ ）
    A.（﹣∞，﹣1）∪（0，1）
    B.（﹣1，0）∪（1，+∞）
    C.（﹣∞，﹣1）∪（﹣1，0）
    D.（0，1）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知三棱柱A1B1C1﹣ABC中，侧棱与底面垂直，AB=BC=AA1 ， ∠ABC=90°，M是BC的中点．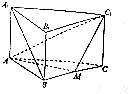

    （1）求证：A1B∥平面AMC1；
    （2）求平面A1B1M与平面AMC1所成角的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=|x﹣ |+|x+m|（m＞0）
    （1）证明：f（x）≥4；
    （2）若f（2）＞5，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，输出的结果为1538，则判断框内可填入的条件为（ ）

    A.n＞6？
    B.n＞7？
    C.n＞8？
    D.n＞9？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（分）已知椭圆的左焦点为，过的直线与交于、两点．

    （）求椭圆的离心率．

    （）当直线与轴垂直时，求线段的长．

    （）设线段的中点为，为坐标原点，直线交椭圆交于、两点，是否存在直线使得？若存在，求出直线的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆心在轴上的圆与直线切于点.圆： ．

    （1）求圆的标准方程；

    （2）已知，圆与轴相交于两点（点在点的右侧）．过点任作一条倾斜角不为0的直线与圆相交于两点．问：是否存在实数，使得？若存在，求出实数的值，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案