
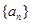 ,把
,把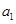 作为新数列
作为新数列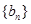 的第一项,把
的第一项,把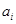 或
或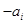 (
(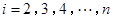 )作为新数列
)作为新数列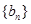 的第
的第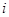 项,数列
项,数列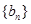 称为数列
称为数列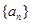 的一个生成数列.例如,数列
的一个生成数列.例如,数列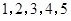 的一个生成数列是
的一个生成数列是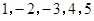 .已知数列
.已知数列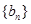 为数列
为数列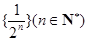 的生成数列,
的生成数列,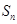 为数列
为数列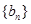 的前
的前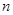 项和.
项和.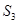 的所有可能值;
的所有可能值;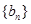 满足
满足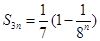 ,求数列
,求数列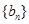 的通项公式;
的通项公式;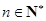 ,
,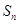 的所有可能值组成的集合为
的所有可能值组成的集合为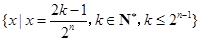 .
.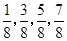 (2)
(2)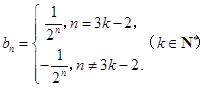 (3)详见解析.
(3)详见解析.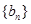 所有可能情况,共
所有可能情况,共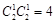 种,分别计算和值为
种,分别计算和值为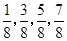 ,本题目的初步感观生成数列
,本题目的初步感观生成数列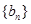 (2)已知和项解析式,则可利用
(2)已知和项解析式,则可利用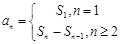 求通项. 当
求通项. 当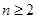 时,
时, ,而
,而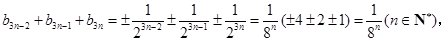 当且仅当
当且仅当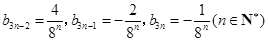 时,才成立.所以
时,才成立.所以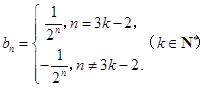 (3)本题实际是对(1)的推广.证明的实质是确定集合
(3)本题实际是对(1)的推广.证明的实质是确定集合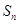 的个数及其表示形式.首先集合
的个数及其表示形式.首先集合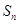 的个数最多有
的个数最多有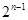 种情形,而每一种的值都不一样,所以个数为
种情形,而每一种的值都不一样,所以个数为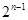 种情形,这是本题的难点,利用同一法证明. 确定集合
种情形,这是本题的难点,利用同一法证明. 确定集合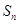 的表示形式,关键在于说明分子为奇数.由
的表示形式,关键在于说明分子为奇数.由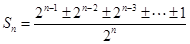 得分子必是奇数,奇数个数由范围
得分子必是奇数,奇数个数由范围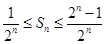 确定.
确定.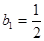 ,
,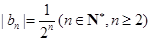 ,
,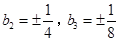 ,
,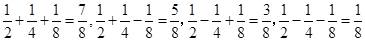 ,
,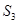 可能值为
可能值为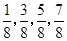 . 3分
. 3分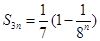 ,
,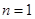 时,
时,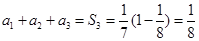 ,
,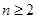 时,
时,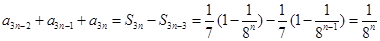 ,
,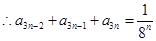 ,
,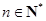 , 5分
, 5分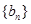 是
是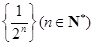 的生成数列,
的生成数列,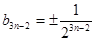 ;
;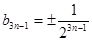 ;
;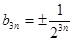 ;
;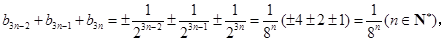
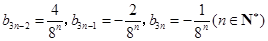 时,才成立.
时,才成立.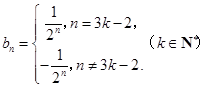 . 8分
. 8分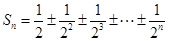 共有
共有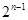 种情形.
种情形.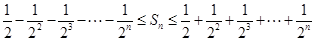 ,即
,即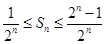 ,
, 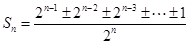 ,分子必是奇数,
,分子必是奇数,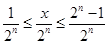 的奇数
的奇数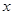 共有
共有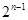 个. 10分
个. 10分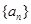 与数列
与数列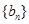 为两个生成数列,数列
为两个生成数列,数列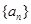 的前
的前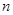 项和为
项和为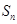 ,数列
,数列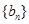 的前
的前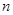 项和为
项和为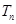 ,从第二项开始比较两个数列,设第一个不相等的项为第
,从第二项开始比较两个数列,设第一个不相等的项为第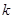 项.
项.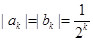 ,不妨设
,不妨设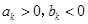 ,
,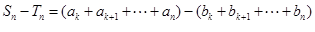
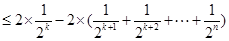
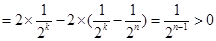 ,
,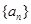 与数列
与数列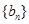 的前
的前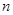 项完全相同时,才有
项完全相同时,才有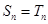 .12分
.12分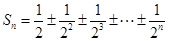 共有
共有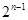 种情形,其值各不相同.
种情形,其值各不相同.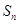 可能值必恰为
可能值必恰为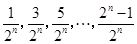 ,共
,共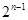 个.
个.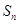 所有可能值集合为
所有可能值集合为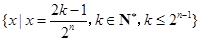 . 13分
. 13分

科目:高中数学 来源:不详 题型:解答题
 }的首项为
}的首项为 a
a .设数列的前n项和为Sn,且对任意正整数n都有
.设数列的前n项和为Sn,且对任意正整数n都有 .
. }的通项公式及Sn;
}的通项公式及Sn; 成等比数列?若存在,求出n和k的值;若不存在,请说明理由.
成等比数列?若存在,求出n和k的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 级需要的天数为
级需要的天数为 ,
,| 等级 | 等级图标 | 需要天数 | 等级 | 等级图标 | 需要天数 |
| 1 |  | 5 | 7 |     | 77 |
| 2 |   | 12 | 8 |   | 96 |
| 3 |    | 21 | 12 |    | 192 |
| 4 |  | 32 | 16 |  | 320 |
| 5 |   | 45 | 32 |   | 1152 |
| 6 |    | 60 | 48 |    | 2496 |
 级需要的天数
级需要的天数 __________
__________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com