
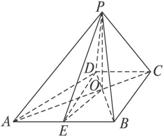
(1)求异面直线PD与BC所成角的余弦值;
(2)求二面角P-AB-C的大小;
(3)设点M在棱PC上,且![]() =λ,问λ为何值时,PC⊥平面BMD?
=λ,问λ为何值时,PC⊥平面BMD?
解法一:∵PO⊥平面ABCD,∴PO⊥BD.
又PB⊥PD,BO=2,PO=![]() ,
,

由平面几何知识得OD=1,PD=![]() ,PB=
,PB=![]() .
.
(1)过D作DE∥BC交AB于E.
连结PE,则∠PDE或其补角为异面直线PD与BC所成的角.
∵四边形ABCD是等腰梯形,
∴OC=OD=1,OB=OA=2,OA⊥OB.
∴BC=![]() ,AB=2
,AB=2![]() ,CD=
,CD=![]() .
.
又AB∥DC,
∴四边形EBCD是平行四边形.
∴ED=BC=![]() ,BE=CD=
,BE=CD=![]() .
.
∴E是AB的中点,且AE=![]() .
.
又PA=PB=![]() ,∴△PEA为直角三角形.
,∴△PEA为直角三角形.
∴PE=![]() =2.
=2.
在△PED中,由余弦定理得
cos∠PDE=![]() .
.
故异面直线PD与BC所成的角的余弦值为![]() .
.
(2)连结OE,由(1)及三垂线定理,知∠PEO为二面角P-AB-C的平面角.
∴sin∠PEO=![]() .∴∠PEO=45°.
.∴∠PEO=45°.
∴二面角P-AB-C的大小为45°.
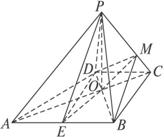
(3)连结MD、MB、MO,
∵PC⊥平面BMD,OM![]() 平面BMD,∴PC⊥OM.
平面BMD,∴PC⊥OM.
又在Rt△POC中,
PC=PD=![]() ,OC=1,PO=
,OC=1,PO=![]() ,
,
∴PM=![]() ,MC=
,MC=![]() .∴
.∴![]() 2.
2.
故λ=2时,PC⊥平面BMD.
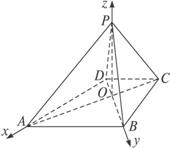
解法二:∵PO⊥平面ABCD,∴PO⊥BD.
又PB⊥PD,BO=2,PO=![]() ,
,
由平面几何知识得OD=OC=1,BO=AO=2.
以O为原点,OA、OB、OP分别为x、y、z轴建立如图所示的空间直角坐标系,则各点坐标为O(0,0,0),A(2,0,0),B(0,2,0),C(-1,0,0),D(0,-1,0),P(0,0,![]() ).
).
(1)∵![]() =(0,-1,
=(0,-1,![]() ),
),![]() =(-1,-2,0),
=(-1,-2,0),
∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,![]() ·
·![]() =2.
=2.
∴cos〈![]() ,
,![]() 〉=
〉=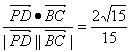 .
.
故直线PD与BC所成的角的余弦值为![]() .
.
(2)设平面PAB的一个法向量为n=(x,y,z),
由于![]() =(-2,2,0),
=(-2,2,0),![]() =(-2,0,
=(-2,0,![]() ),
),
由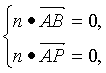 得
得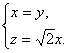
取n=(1,1,![]() ),
),
又易知平面ABCD的一个法向量m=(0,0,1),
∴cos〈m,n〉=![]() .
.
又二面角P-AB-C为锐角,
∴所求二面角P-AB-C的大小为45°.
(3)设M(x0,0,z0),由于P、M、C三点共线,
z0=![]() , ①
, ①
∵PC⊥平面BMD,∴OM⊥PC.
∴(-1,0,![]() )·(x0,0,z0)=0.
)·(x0,0,z0)=0.
∴x0+![]() z0=0. ②
z0=0. ②
由①②知x0=![]() ,z0=
,z0=![]() .
.
∴M(![]() ,0,
,0,![]() ).∴λ=
).∴λ=![]() =2.
=2.
故λ=2时,PC⊥平面BMD.


科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.8
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,| PN |
| 1 |
| 2 |
| NC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com