解:(1)曲线y=x
2-2x-3与y轴的交点为(0,3),
与x轴的交点为(-1,0),(3,0),
设圆C的圆心为(1,t),
则有1
2+(t+3)
2=(1+1)
2+t
2,解得t=-1.
则圆C的半径为

,
∴圆C的方程为(x-1)
2+(y+1)
2=5.
(2)∵|AB|=2

,
∴圆心C到直线x-y+a=0的距离为

,
∴
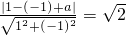
,解得a=0,或a=-4.
(3)设A(x
1,y
1),B(x
2,y
2),其坐标满足方程组
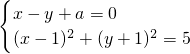
,
消去y,得2x
2+2ax+a
2+2a-3=0.
∵圆C与直线x-y+a=0交于A,B两点,
∴△=24-16a-4a
2>0,
∴x
1+x
2=-a,x
1x
2=
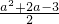
.①
由于OA⊥OB,∴x
1x
2+y
1y
2=0,
∵y
1=x
1+a,y
2=x
2+a,
∴2x
1x
2+a(x
1+x
2)+a
2=0.②
由①②,得a=1,或a=-3.满足△>0,
故a=1,或a=-3.
分析:(1)曲线y=x
2-2x-3与y轴的交点为(0,3),与x轴的交点为(-1,0),(3,0),设圆C的圆心为(1,t),解得t=-1.由此能求出圆C的方程.
(2)由|AB|=2

,知圆心C到直线x-y+a=0的距离为

,由点到直线的距离公式能求出a的值.
(3)设A(x
1,y
1),B(x
2,y
2),由
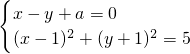
,得2x
2+2ax+a
2+2a-3=0.由OA⊥OB,能求出a的值.
点评:本题考查圆的方程的求法,考查满足条件的a的值的求法,解题时要认真审题,仔细解答,注意点到直线的距离公式、韦达定理、根的判别式、向量等知识点的合理运用.

 ,求a的值;
,求a的值; ,
, ,
, ,
,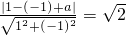 ,解得a=0,或a=-4.
,解得a=0,或a=-4.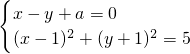 ,
,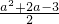 .①
.① ,知圆心C到直线x-y+a=0的距离为
,知圆心C到直线x-y+a=0的距离为 ,由点到直线的距离公式能求出a的值.
,由点到直线的距离公式能求出a的值.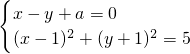 ,得2x2+2ax+a2+2a-3=0.由OA⊥OB,能求出a的值.
,得2x2+2ax+a2+2a-3=0.由OA⊥OB,能求出a的值.
