
| 甲 | 乙 | ||||||||||||||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 | ||||||||||||
| 概率 |
|
|
|
概率 |
|
|
| ||||||||||||
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 2 |
| 1 |
| 6 |
| C | 2 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 1 |
| 6 |
| 7 |
| 162 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 18 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |
| 18 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 18 |
| 2 |
| 9 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 18 |
| 1 |
| 9 |
| 5 |
| 18 |
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 18 |
| 107 |
| 6 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
| 射手甲 | 射手乙 | ||||||||||||||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 | ||||||||||||
| 概率 |
|
|
|
概率 |
|
|
| ||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
射手甲 |
| 射手乙 | ||||||
环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 | |
概率 |
|
|
| 概率 |
|
|
| |
(I)若甲射手共有5发子弹,一旦命中10环就停止射击,求他剩余3颗子弹的概率;
(Ⅱ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅲ)若两个射手各射击1次,记所得的环数之和为![]() ,求
,求![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省五校协作体高三上学期期初联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
|
射手甲 |
射手乙 |
||||||
|
环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
|
概率 |
|
|
|
概率 |
|
|
|
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为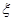 ,求
,求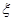 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源:福建省09-10学年高二下学期期末数学理科考试试题 题型:解答题
(本小题满分13分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:K^S*5U.C#O%
|
射手甲 |
射手乙 |
||||||
|
环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
|
概率 |
|
|
|
概率 |
|
|
|
(1)若甲射手共有5发子弹,一旦命中10环就停止射击,求他剩余3颗子弹的概率;
(2)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;K^S*5U.C#O%
(3)若两个射手各射击1次,记所得的环数之和为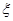 ,求
,求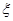 的分布列和期望。
的分布列和期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com