
(理科)已知函数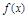 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若y=f(x)在[-1,1]上存在零点,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).
(Ⅰ):因为函数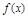 =x2-4x+a+3的对称轴是x=2,
=x2-4x+a+3的对称轴是x=2,
所以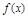 在区间[-1,1]上是减函数,
在区间[-1,1]上是减函数,
因为函数在区间[-1,1]上存在零点,则必有:
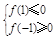 即
即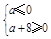 ,解得
,解得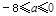 ,
,
故所求实数a的取值范围为[-8,0] .
(Ⅱ)若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,只需函数y=f(x)的值域为函数y=g(x)的值域的子集.
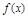 =x2-4x+3,x∈[1,4]的值域为[-1,3],下求g(x)=mx+5-2m的值域.
=x2-4x+3,x∈[1,4]的值域为[-1,3],下求g(x)=mx+5-2m的值域.
①当m=0时,g(x)=5-2m为常数,不符合题意舍去;
②当m>0时,g(x)的值域为[5-m,5+2m],要使[-1,3] [5-m,5+2m],
[5-m,5+2m],
需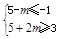 ,解得m≥6;
,解得m≥6;
③当m<0时,g(x)的值域为[5+2m,5-m],要使[-1,3] [5+2m,5-m],
[5+2m,5-m],
需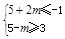 ,解得m≤-3;
,解得m≤-3;
综上,m的取值范围为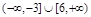 .
.
(Ⅲ)由题意知 ,可得
,可得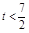 .
.
①当t≤0时,在区间[t,4]上,f(t)最大,f(2)最小,
所以f(t)-f(2)=7-2 t即t2-2t-3=0,解得t=-1或t=3(舍去);
②当0<t≤2时,在区间[t,4]上,f(4)最大,f(2)最小,
所以f(4)-f(2)=7-2 t即4=7-2t,解得t= ;
;
③当2<t<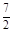 时,在区间[t,4]上,f(4)最大,f(t)最小,
时,在区间[t,4]上,f(4)最大,f(t)最小,
所以f(4)-f(t)=7-2t即t2-6t+7=0,解得t=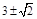 (舍去)
(舍去)
综上所述,存在常数t满足题意,t=-1或 .
.
【解析】略


科目:高中数学 来源:云南省昆明一中2007届高三年级上学期第四次月考 数学试题 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:四川省成都外国语学校2012届高三12月月考数学试题 题型:044
(理科)已知函数f(x)=ln(x-1)-k(x-1)+1.
(1)求函数f(x)的单调区间;
(2)若f(x)≤0恒成立,试确定实数k的取值范围;
(3)证明:![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() (n∈N*,且n>1).
(n∈N*,且n>1).
查看答案和解析>>
科目:高中数学 来源:四川省成都外国语学校2012届高三第三次月考数学试题 题型:044
(理科)已知函数f(x)=4x3+3tx2-6t2x+t-1,x∈R,t∈R.
(1)当t≠0时,求f(x)的单调区间;
(2)证明:对任意t∈(0,+∞),f(x)在区间(0,1)内均存在零点.
查看答案和解析>>
科目:高中数学 来源:江苏省泰州中学2012届高三上学期期中考试数学试题(人教版) 题型:044
(理科)已知函数f(x)=ex-kx,x∈R.
(Ⅰ)若k=e,试确定函数f(x)的单调区间;
(Ⅱ)若k>0,且对于任意x∈R,f(|x|)>0恒成立,试确定实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com