【题目】已知数列{an}的前n项和为Sn ， 且 
，数列{bn}满足 
，则数列{anbn}的前n项和Tn= ．
【答案】10+（3n﹣5）2n+1
【解析】解：由已知得，当n≥2时，an=Sn﹣Sn﹣1=（ 
n2﹣ 
n）﹣[ （n﹣1）2﹣ （n﹣1）]=3n﹣2，又a1=1=3×1﹣2，符合上式．
故数列{an}的通项公式an=3n﹣2．
又因为 
，
所以log2bn= 
（an+2）=n，即bn=2n ，
令cn=anbn ．
则cn=（3n﹣2）2n ．
所以Tn=1×21+422+723+…+（3n﹣2）2n ， ①
2Tn=1×22+4×23+724+…+（3n﹣2）2n+1 ， ②
由②﹣①得：﹣Tn=2+322+323+…+（3n﹣5）2n+1=3×（2+22+…+2n）﹣（3n﹣2）2n+1﹣2
=﹣（3n﹣5）2n+1﹣10，
所以Tn=10+（3n﹣5）2n+1
故答案是：10+（3n﹣5）2n+1 ．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系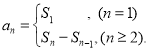
才能正确解答此题．
53随堂测系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
其中P，M是非空数集，且P∩M=，设f（P）={y|y=f（x），x∈P}，f（M）={y|y=f（x），x∈M}．
（I）若P=（﹣∞，0），M=[0，4]，求f（P）∪f（M）；
（II）是否存在实数a＞﹣3，使得P∪M=[﹣3，a]，且f（P）∪f（M）=[﹣3，2a﹣3]？若存在，请求出满足条件的实数a；若不存在，请说明理由；
（III）若P∪M=R，且0∈M，I∈P，f（x）是单调递增函数，求集合P，M．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于不等式
，则对区间
上的任意x都成立的实数t的取值范围是_______．
【答案】
【解析】
根据二次函数的单调性求出x2﹣3x+2在区间[0，2]上的最小值和最大值，把问题转化关于t的不等式组
得答案．
∵x2﹣3x+2=
，
∴当x∈[0，2]时，
，（x2﹣3x+2）max=2．
∴
．
∴对于不等式
（2t﹣t2）≤x2﹣3x+2≤3﹣t2，对区间[0，2]上任意x都成立的实数t的取值范围是[﹣1，1﹣
]．
故答案为：[﹣1，1﹣].
【点睛】
本题考查函数恒成立问题，考查了不等式的解法，体现了数学转化思想方法，是基础题．二次不等式分含参二次不等式和不含参二次不等式；对于含参的二次不等式问题，先判断二次项系数是否含参，接着讨论参数等于0，不等于0，再看式子能否因式分解，若能够因式分解则进行分解，再比较两根大小,结合图像得到不等式的解集.
【题型】填空题
【结束】
16
【题目】等差数列{an}的公差d≠0满足
成等比数列，若
=1，Sn是{
}的前n项和，则
的最小值为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】曲线C1的参数方程为
(θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的
倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.
(1)求曲线C2和直线l的普通方程.
(2)P为曲线C2上任意一点,求点P到直线l的距离的最值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从1至9这9个自然数中任取两个：
恰有一个偶数和恰有一个奇数；
至少有一个是奇数和两个数都是奇数；
至多有一个奇数和两个数都是奇数；
至少有一个奇数和至少有一个偶数．
在上述事件中，是对立事件的是
A. B. 
C. D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义在R上的函数f（x），满足 
，且f（3）=f（1）﹣1．
（1）求实数k的值；
（2）若函数g（x）=f（x）+f（﹣x）（﹣2≤x≤2），求g（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】用长为18 cm的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2：1，问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知：函数
，当x∈（－3，2）时，
>0，当x∈（－
，－3）
（2，+）时，<0
（I）求a，b的值；
（II）若不等式
的解集为R，求实数c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
