
分析 (Ⅰ)把参数方程、极坐标方程分别化为直角坐标方程,联立解出交点坐标,再化为极坐标即可得出.
(Ⅱ)由(Ⅰ)可得公共弦所在的直线方程为:y=x.可得直线l的斜率为-1.利用点斜式可得直角坐标方程,再化为极坐标方程.
解答 解:(Ⅰ)圆C1的极坐标方程是ρ2+2ρcosθ=0,直角坐标方程为x2+y2+2x=0,
圆C2的参数方程是$\left\{\begin{array}{l}{x=cosα}\\{y=-1+sinα}\end{array}\right.$(α是参数),普通方程为x2+(y+1)2=1.
C1和C2的交点的坐标为(0,0),(-1,-1),极坐标(0,0),($\sqrt{2}$,$\frac{5π}{4}$);
(Ⅱ)由(Ⅰ)可得公共弦所在的直线方程为:y=x.
∴直线l的斜率为-1.
直线l经过交点(0,0)时,直线l的方程为:y=-x,可得极坐标:θ=$\frac{3π}{4}$(ρ∈R).
直线l经过交点(-1,-1)时,直线l的方程为:y+1=-(x+1),
即x+y+2=0,可得极坐标:ρcosθ+ρsinθ+2=0.
点评 本题考查了极坐标化为直角坐标方程、参数方程化为普通方程、点斜式、相互垂直的直线斜率之间的关系、曲线的交点,考查了推理能力与计算能力,属于中档题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
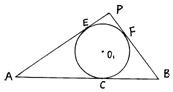 如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.
如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com