
 是两个互相垂直的单位向量,已知向量
是两个互相垂直的单位向量,已知向量 且向量
且向量 ,
, .
. ,
,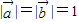 可求
可求 =2k,
=2k, =
= ,
, ,代入f(k)=cosθ=
,代入f(k)=cosθ= 可求
可求
 ,可求k
,可求k =
=
 ?
? ,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解
,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解 ∴
∴ ,
,
 =
= =2k
=2k =
= ,同理可得
,同理可得
 =
= (k>0)…(4分)
(k>0)…(4分)
 (8分)
(8分) )=
)= =
=

 ,
,
 };
};

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com