Question

某工厂为了提高经济效益，决定花5600千元引进新技术，同时适当进行裁员．已知这家公司现有职工m人，每人每年可创利100千元．据测算，若裁员人数不超过现有人数的20%，则每裁员1人，留岗员工每人每年就能多创利1千元；若裁员人数超过现有人数的20%，则每裁员1人，留岗员工每人每年就能多创利2千元．为保证公司的正常运转，留岗的员工数不得少于现有员工人数的75%．为保障被裁员工的生活，公司要付给被裁员工每人每年20千元的生活费．
（1）若m=400时，要使公司利润至少增加10%，那么公司裁员人数应在什么范围内？
（2）若m=20k，且15＜k＜50，为了获得最大的经济效益，该公司应裁员多少人？

Answer 1

解：设该公司应裁员x人，x∈N^*，所获得利润为y．
（1）m=400时，若0≤x≤80
公司所获利润y=（400-x）（100+x）-20x-5600
要使公司利润至少增加10%那么（400-x）（100+x）-20x-5600≥400×100×（1+10%）x²-280x+9600≤0又0≤x≤80所以40≤x≤80．
若80≤x≤100公司所获利润y=（400-x）（100+2x）-20x-5600
要使公司利润至少增加10%那么（400-x）（100+2x）-20x-5600≥400×100×（1+10%）x²-340x+4800≤0它在80≤x≤100时成立
所以40≤x≤100时公司利润至少增加10%．
（2）设公司裁员x人，所获得利润为y千元．则

=
=
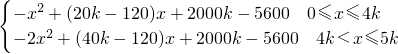
设f₁（x）=-（x-（10k-60））²+2000k-5600+（10k-60）²，0≤x≤4k，
因为10k-60＞150-60=90＞4k．所以当x=4k时，函数f₁（x）取最大值为：
f₁（x）_max=64k²+80k-5600．
设f₂（x）=-2（x-（10k-30））²+2000k-5600+2（10k-30）²，4k＜x≤5k，
因为10k-30＞150-30=120＞5k．所以当x=5k时，函数f₂（x）取最大值为：
f₁（x）_max=150k²+50k-5600．f₂（x）-f₁（x）=86k²-30k＞0．
所以当x=5k时公司可获得最大利润．
分析：（1）根据已知条件，当m=400时，我们根据若裁员人数超过现有人数的20%，则每裁员1人，留岗员工每人每年就能多创利2千元．为保证公司的正常运转，留岗的员工数不得少于现有员工人数的75%．设该公司应裁员x人，我们分0≤x≤80，80≤x≤100两种情况分析讨论公司所获利润，然后列出公司利润至少增加10%的对应的不等式，解不等式，即可得到公司裁员人数的取值范围．
（2）当m=20k，时，我们根据（1）中的分析，分0≤x≤4k，4k＜x≤5k，两种情况分析讨论公司所获利润，然后在构造出公司利润与栽员人数之间的分段函数的解析式，然后在每一段上，分析函数的最值，进而得到合理的裁员方案．
点评：函数的实际应用题，我们要经过析题→建模→解模→还原四个过程，在建模时要注意实际情况对自变量x取值范围的限制，解模时也要实际问题实际考虑．将实际的最大（小）化问题，利用函数模型，转化为求函数的最大（小）是最优化问题中，最常见的思路之一．