
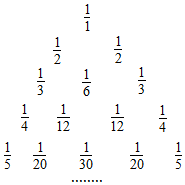
 如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$. 分析 根据“莱布尼兹调和三角形”的特征,每个数是它下一个行左右相邻两数的和,得出将杨晖三角形中的每一个数Cnr都换成分数$\frac{1}{(n+1){C}_{n}^{r}}$,就得到一个莱布尼兹三角形,从而可求出第n(n≥4)行倒数第四个数(从右往左数).
解答 解:将杨晖三角形中的每一个数Cnr都换成分数$\frac{1}{(n+1){C}_{n}^{r}}$,
就得到莱布尼兹三角形.
∵杨晖三角形中第n(n≥4)行倒数第四个数(从右往左数)Cn-13,
则“莱布尼兹调和三角形”第n(n≥4)行倒数第四个数(从右往左数)是$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.
故答案为:$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.
点评 本题考查归纳推理,解题的关键是通过观察分析归纳各数的关系,考查学生的观察分析和归纳能力,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
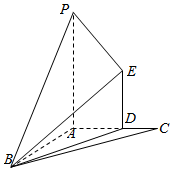 平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a | B. | 2a2-2b2-4b | C. | 4a或2a2-2b2-4b | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com