
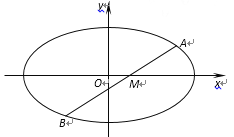
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() . 已知过点
. 已知过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值.若存在,求出点
为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)先根据已知得到三个方程解方程组即得椭圆C的方程. (2) 设N(n,0),先讨论l斜率不存在的情况得到n=4,再证明当N为(4,0)时,对斜率为k的直线l:y=k(x-![]() ),恒有
),恒有![]() =12.
=12.
详解:(1)离心率e=![]() ,所以c=
,所以c=![]() a,b=
a,b=![]() =
=![]() a,
a,
所以椭圆C的方程为![]() .
.
因为椭圆C经过点![]() ,所以
,所以![]() \,
\,
所以b2=1,所以椭圆C的方程为![]() .
.
(2)设N(n,0),
当l斜率不存在时,A(![]() ,y),B(
,y),B(![]() ,-y),则y2=1-
,-y),则y2=1-![]() =
=![]() ,
,
则![]() =(
=(![]() -n)2-y2=(
-n)2-y2=(![]() -n)2-
-n)2-![]() =n2-
=n2-![]() n-
n-![]() ,
,
当l经过左右顶点时,![]() =(-2-n)(2-n)=n2-4.
=(-2-n)(2-n)=n2-4.
令n2-![]() n-
n-![]() =n2-4,得n=4.
=n2-4,得n=4.
下面证明当N为(4,0)时,对斜率为k的直线l:y=k(x-![]() ),恒有
),恒有![]() =12.
=12.
设A(x1,y1),B(x2,y2),
由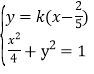 消去y,得(4k2+1)x2-
消去y,得(4k2+1)x2-![]() k2x+
k2x+![]() k2-4=0,
k2-4=0,
所以x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
所以![]() =(x1-4)(x2-4)+y1y2
=(x1-4)(x2-4)+y1y2
=(x1-4)(x2-4)+k2(x1-![]() )(x2-
)(x2-![]() )
)
=(k2+1)x1x2-(4+![]() k2)(x1+x2)+16+
k2)(x1+x2)+16+![]() k2
k2
=(k2+1) ![]() -(4+
-(4+![]() k2)
k2) ![]() +16+
+16+![]() k2
k2
=![]() +16=12.
+16=12.
所以在x轴上存在定点N(4,0),使得![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】某学校微信公众号收到非常多的精彩留言,学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:
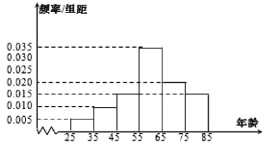
(1)求这100位留言者年龄的平均数和中位数;
(2)学校从参加调查的年龄在![]() 和
和![]() 的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在
的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在![]() 的留言者每人一部价值1000元的手机,年龄在
的留言者每人一部价值1000元的手机,年龄在![]() 的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.
的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个部件由三个元件按如图所示的方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()
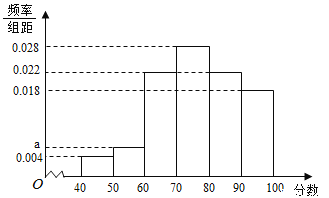
(1)求频率分布图中![]() 的值,并估计该企业的职工对该部门评分不低于80的概率;
的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率..
的概率..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1) 求函数![]() 的反函数
的反函数![]() ;
;
(2)试问:函数![]() 的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
(3)若方程![]() 的三个实数根
的三个实数根![]() 满足:
满足: ![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
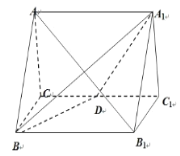
【题目】如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥平面A1BD;
(2)求锐二面角A-A1D-B的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张先生2018年年底购买了一辆![]() 排量的小轿车,为积极响应政府发展森林碳汇(指森林植物吸收大气中的二氧化碳并将其固定在植被或土壤中)的号召,买车的同时出资1万元向中国绿色碳汇基金会购买了 2亩荒山用于植树造林.科学研究表明:轿车每行驶3000公里就要排放1吨二氧化碳,林木每生长1立方米,平均可吸收1.8吨二氧化碳.
排量的小轿车,为积极响应政府发展森林碳汇(指森林植物吸收大气中的二氧化碳并将其固定在植被或土壤中)的号召,买车的同时出资1万元向中国绿色碳汇基金会购买了 2亩荒山用于植树造林.科学研究表明:轿车每行驶3000公里就要排放1吨二氧化碳,林木每生长1立方米,平均可吸收1.8吨二氧化碳.
(1)若张先生第一年(即2019年)会用车1.2万公里,以后逐年増加1000公里,则该轿车使用10年共要排放二氧化碳多少吨?
(2)若种植的林木第一年(即2019年)生长了1立方米,以后每年以10%的生长速度递增,问林木至少生长多少年,吸收的二氧化碳的量超过轿车使用10年排出的二氧化碳的量(参考数据:![]() ,
,![]() ,
,![]() )?
)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com